【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,同时直线PQ由点B出发,沿BA的方向匀速运动,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t≤5).线段CM的长度记作y甲 , 线段BP的长度记作y乙 , y甲和y乙关于时间t的函数变化情况如图所示.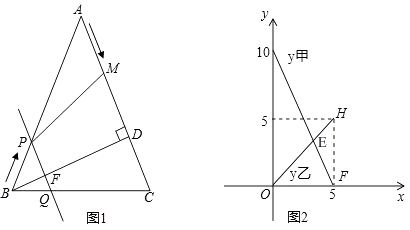
(1)由图2可知,点M的运动速度是每秒cm,当t为何值时,四边形PQCM是平行四边形?在图2中反映这一情况的点是;
(2)设四边形PQCM的面积为ycm2 , 求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PQCM= ![]() S△ABC?若存在,求出t的值;若不存在,说明理由;
S△ABC?若存在,求出t的值;若不存在,说明理由;
(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
参考答案:
【答案】
(1)2,E( ![]() ,
,![]() )
)
(2)解:∵PQ∥AC,
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴ ![]() ,即
,即 ![]() ,
,
解得:BF= ![]() t,
t,
∴FD=BD﹣BF=8﹣ ![]() t,
t,
又∵MC=AC﹣AM=10﹣2t,
∴y= ![]() (PQ+MC)FD=
(PQ+MC)FD= ![]() (t+10﹣2t)(8﹣
(t+10﹣2t)(8﹣ ![]() t)=
t)= ![]() t2﹣8t+40;
t2﹣8t+40;
(3)解:存在;
∵S△ABC= ![]() ACBD=
ACBD= ![]() ×10×8=40,
×10×8=40,
当S四边形PQCM= ![]() S△ABC时,y=
S△ABC时,y= ![]() t2﹣8t+40=20,
t2﹣8t+40=20,
解得:t=10﹣5 ![]() ,或t=10+5
,或t=10+5 ![]() (不合题意,舍);
(不合题意,舍);
即:t=10﹣5 ![]() 时,S四边形PQCM=
时,S四边形PQCM= ![]() S△ABC.
S△ABC.
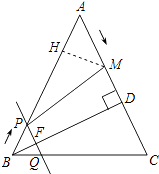
(4)解:假设存在某一时刻t,使得M在线段PC的垂直平分线上,则MP=MC,
过M作MH⊥AB,交AB与H,如图所示:
∵∠A=∠A,∠AHM=∠ADB=90°,
∴△AHM∽△ADB,
∴ ![]() ,
,
又∵AD=6,
∴ ![]() ,
,
∴HM= ![]() t,AH=
t,AH= ![]() t,
t,
∴HP=10﹣t﹣ ![]() t=10﹣
t=10﹣ ![]() t,
t,
在Rt△HMP中,MP2=( ![]() t)2+(10﹣
t)2+(10﹣ ![]() t)2=
t)2= ![]() t2﹣44t+100,
t2﹣44t+100,
又∵MC2=(10﹣2t)2=100﹣40t+4t2,
∵MP2=MC2,
∴ ![]() t2﹣44t+100=100﹣40t+4t2,
t2﹣44t+100=100﹣40t+4t2,
解得 t1= ![]() ,t2=0(舍去),
,t2=0(舍去),
∴t= ![]() s时,点M在线段PC的垂直平分线上.
s时,点M在线段PC的垂直平分线上.
【解析】解:(1)由图2得,点M的运动速度为2cm/s,PQ的运动速度为1cm/s,
∵四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10﹣t=2t,
解得:t= ![]() ,
,
∴当t= ![]() 时,四边形PQCM是平行四边形,此时,图2中反映这一情况的点是E(
时,四边形PQCM是平行四边形,此时,图2中反映这一情况的点是E( ![]() ,
, ![]() )
)
所以答案是:2,E( ![]() ,
, ![]() ).
).
【考点精析】通过灵活运用相似三角形的性质,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )

A. 5° B. 15° C. 25° D. 35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:
 ;
;(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OM⊥AB.
(1)∠AOC的邻补角为 (写出一个即可);
(2)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(3)若∠1=
 ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠ADE=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
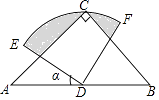
A.由小变大
B.由大变小
C.不变
D.先由小变大,后由大变小 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列判断:
①若|﹣a|=a,则a<0;
②有理数包括整数、0和分数;
③任何正数都大于它的倒数;
④2ax2﹣xy+y2是三次三项式;
⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负.
上述判断正确的有( )
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.

相关试题

