【题目】阅读并解答问题:
明朝数学家程大位在其数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”问题:原文:平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?译文:如图,有一架秋千,当它静止时,踏板离地![]() 尺,将它往前推送
尺,将它往前推送![]() 尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为
尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为![]() 尺,秋千的绳索始终拉得很直,试问绳索有多长?(注:古代
尺,秋千的绳索始终拉得很直,试问绳索有多长?(注:古代![]() 尺为
尺为![]() 步)
步)

建立数学模型:如图,秋千绳索![]() 静止的时候,踏板离地高
静止的时候,踏板离地高![]() 尺(
尺(![]() 尺),将它往前推进两步(
尺),将它往前推进两步(![]() 尺),此时踏板升高离地
尺),此时踏板升高离地![]() 尺(
尺(![]() 尺).已知
尺).已知![]() 于点
于点![]() 于点
于点![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,求秋千绳索(
,求秋千绳索(![]() 或
或![]() )的长度.请解答下列问题:
)的长度.请解答下列问题:
(1)直接写出四边形![]() 是哪种特殊的四边形;
是哪种特殊的四边形;
(2)求![]() 的长.
的长.
参考答案:
【答案】(1)四边形![]() 是矩形;(2)秋千绳索
是矩形;(2)秋千绳索![]() 的长度为
的长度为![]() 尺
尺
【解析】
(1)根据有三个角是直角的四边形是矩形,即可得出结论;
(2)设绳索OA=OB=x,根据题意可得OE=(x-4)尺,利用勾股定理即可得![]() ,解方程即可求解.
,解方程即可求解.
解:![]() 四边形
四边形![]() 是矩形
是矩形
理由:∵OC⊥CD,BD⊥CD,BE⊥OC
∴∠ECD=∠BDC=∠BEC=90°,
∴四边形ECDB是矩形;
![]() 设
设![]() 尺,
尺,
![]()
![]()
在![]() 中,
中,![]()
根据勾股定理,得![]()
整理,得![]()
解得![]()
答:秋千绳索![]() 的长度为
的长度为![]() 尺
尺
-
科目: 来源: 题型:
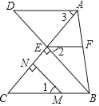
查看答案和解析>>【题目】如图,BE⊥AC与点E,MN⊥AC于点N,∠1=∠2,∠3=∠C,若∠AFE=80°,求∠DAF的度数.请根据解题过程“填空”或“说明理由”.
解:∵BE⊥AC,MN⊥AC
∴BE∥MN
∴∠1= ( )
又∵∠1=∠2
∴∠2= ( )
∴EF∥BC( )
∵∠3=∠C
∴AD∥BC
∴AD∥EF
∴∠DAF+∠AFE=180°( )
∴∠DAF=180°﹣∠AFE=180°﹣80°=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号).
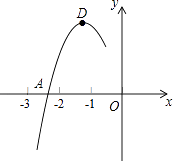
-
科目: 来源: 题型:
查看答案和解析>>【题目】聪聪在给妈妈过生日时发现自己的年龄与妈妈的年龄的十位数字与个位数字正好相反,他同时还发现,过10年,妈妈岁数减1(岁)刚好是自己岁数加1(岁)的2倍;再过1年,他们两人的年龄又一次相反,且十位数字与个位数字的和为7,你能知道聪聪和他妈妈现在的年龄吗?
(1)设未知数,用代数式表示聪聪和他妈妈的年龄;
(2)列方程解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备为七年级同学庆祝最后一个“儿童节”,至少需要甲种鲜花266朵,乙种鲜花169朵,制成A、B两种造型共16束.要求A造型用甲种鲜花18朵,乙种鲜花10朵;B造型用甲种鲜花16朵,乙种鲜花11朵,送某花店制作.
(1)花店共有几种制作方案?分别有哪几种?
(2)若A种造型每束鲜花可获得利润12元,B种造型每束鲜花可获得利润10元.如果你是店主,你选择哪种制作方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,若点
,若点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿折线
个单位长度的速度沿折线 运动(回到点
运动(回到点 停止运动),设运动时间为
停止运动),设运动时间为 秒.
秒.(1)当点
 在
在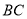 上时,且满足
上时,且满足 时,求出此时
时,求出此时 的值;
的值;(2)当点
 在
在 上时,求出
上时,求出 为何值时,
为何值时, 为以
为以 为腰的等腰三角形.
为腰的等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x+
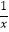 =3,则下列三个等式:①x2+
=3,则下列三个等式:①x2+ 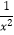 =7,②x﹣
=7,②x﹣ 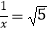 ,③2x2﹣6x=﹣2中,正确的个数有( )
,③2x2﹣6x=﹣2中,正确的个数有( )
A.0个
B.1个
C.2个
D.3个
相关试题

