【题目】如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( ) 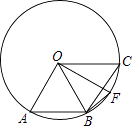
A.12.5°
B.15°
C.20°
D.22.5°
参考答案:
【答案】B
【解析】解:∵四边形ABCO是平行四边形, ∴AB=BC,OA∥BC.
∵OA=OC,
∴△OAB是等边三角形,
∴∠AOB=60°.
∵OF⊥OA,
∴∠AOF=90°,OF⊥BC,
∴∠BOF=∠COF=90°﹣60°=30°,
∴∠CBF= ![]() ∠COF=15°.
∠COF=15°.
故选B.
【考点精析】通过灵活运用平行四边形的性质和垂径定理,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P的坐标为(a,b),点P的“变换点”P`的坐标定义如下:当
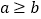 时,P`点坐标为(a,-b);当
时,P`点坐标为(a,-b);当 时,P`点坐标为(b,-a)。线段l:
时,P`点坐标为(b,-a)。线段l: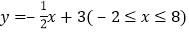 上所有点按上述“变换点”组成一个新的图形,若直线
上所有点按上述“变换点”组成一个新的图形,若直线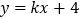 与组成的新的图形有两个交点,则k的取值范围是( )
与组成的新的图形有两个交点,则k的取值范围是( )A.
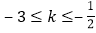 B.
B.  或
或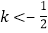 C.
C. 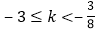 D.
D. 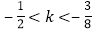
-
科目: 来源: 题型:
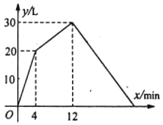
查看答案和解析>>【题目】一个装有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间(单价:min)之间的关系如图所示。在第_______分钟时该容器内的水恰好为10L.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是( )
A.抛物线的开口向下
B.当x>﹣3时,y随x的增大而增大
C.二次函数的最小值是﹣2
D.抛物线的对称轴是x=﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明本学期的数学测验成绩如表所示:
测验
类别
平时测验
期中
测验
期末
测验
第1次
第2此
第3次
第4次
成绩
80
86
84
90
90
95
(1)求六次测验成绩的众数和中位数;
(2)求小明本学期的数学平时测验的平均成绩;
(3)如果本学期的总评成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照3:3:4的比例计算所得,计算小明本学期学科的总评成绩。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E是AD的中点,延长CB到点F,使
 ,连接BE、AF.
,连接BE、AF.(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划从某苗木基地购进A、B两咱树苗共200棵绿化校园。已知购买了3棵A种树苗和5棵B种树苗共需700元;购买2棵A种树苗和1棵B种树苗共需280元.
(1)每棵A种树苗、B种树苗各需多少元?
(2)学校除支付购买树苗的费用外,平均每棵树苗还需支付运输及种植费用20元。设学校购买B种树苗x棵,购买两种树苗及运输、种植所需的总费用为y元,求y与x的函数关系;
(3)在(2)的条件下,若学校用于绿化的总费用在22400元限额内,且购买A种树苗的数量不少于B种树苗的数量,请给出一种费用最省的方案,并求出该方案所需的费用.
相关试题

