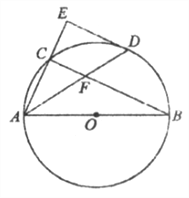
【题目】如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
(1)求证:∠BAD=∠DAE;
(2)若AB=6,AD=5,求DF的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析:(1)连接OD,由ED为⊙O的切线,根据切线的性质得到OD⊥ED,由AB为⊙O的直径,得到∠ACB=90°,根据平行线的判定和性质得到角之间的关系,又因为OA=OD,得到∠BAD=∠ADO,推出结论∠BAD=∠DAE;
(2)连接BD,得到∠ADB=90°,由勾股定理得到![]() ,根据三角函数的定义得到tan∠CBD=tan∠BAD=
,根据三角函数的定义得到tan∠CBD=tan∠BAD=![]() ,由DF=BDtan∠CBD=
,由DF=BDtan∠CBD=![]() .
.
详解:(1)连接OD,
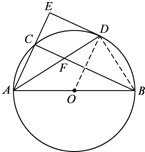
∵ED为⊙O的切线,
∴OD⊥ED,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC∥ED,
∴∠ACB=∠E=∠EDO,
∴AE∥OD,
∴∠DAE=∠ADO,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠BAD=∠DAE;
(2)连接BD,
∴∠ADB=90°,
∵AB=6,AD=5,
∴![]() ,
,
∵∠BAD=∠DAE=∠CBD,
∴tan∠CBD=tan∠BAD=![]() ,
,
在Rt△BDF中,
∴DF=BDtan∠CBD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解:
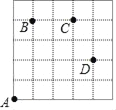
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为鼓励市民节约用水,特制定如下的收费标准:若每月每户用水不超过10立方米,则按3元/立方米的水价收费,并加收0.2元/立方米的污水处理费;若超过10立方米,则超过的部分按4元/立方米的水价收费,污水处理费不变.
(1)若小华家5月份的用水量为8立方米,那么小华家5月份的水费为_______元;
(2)若小华家6月份的用水量为15立方米,那么小华家6月份的水费为_______元;
(3)若小华家某个月的用水量为a(a>10)立方米,求小华家这个月的水费(用含a的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )

A. 4 B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
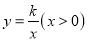 与正比例函数
与正比例函数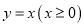 的图象,点
的图象,点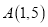 ,点
,点 与点
与点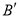 均在反比例函数的图象上,点
均在反比例函数的图象上,点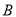 在直线
在直线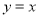 上,四边形
上,四边形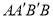 是平行四边形,则
是平行四边形,则 点的坐标为__________.
点的坐标为__________. 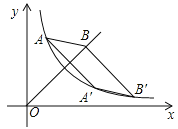
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于有理数
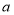 ,
,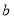 ,定义一种新运算“
,定义一种新运算“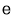 ”,规定
”,规定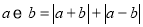 .
.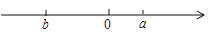
(1)若
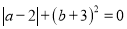 ,计算
,计算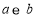 的值.
的值.(2)当
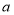 ,
,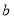 在数轴上的位置如图所示,化简
在数轴上的位置如图所示,化简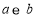 .
.(3)已知
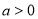 ,
,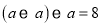 ,求
,求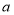 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织七年级学生参加研学活动,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.
(1)求该校此次参加研学活动的学生有多少人?
(2)若单独租用60座的客车,需租_______辆;
(3)已知45座客车的日租金为每辆1 000元,60座客车的日租金为每辆1 200元,该校单独租用哪种车更合算?
相关试题

