【题目】小明和小莉在跑道上进行100 m短跑比赛,两人从出发点同时起跑,小明到达终点时,小莉离终点还差6 m,已知小明和小莉的平均速度分别为x m/s、y m/s.
(1)如果两人重新开始比赛,小明从起点向后退6 m,两人同时起跑能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)如果两人想同时到达终点,应如何安排两人起跑位置?请设计两种方案.
参考答案:
【答案】(1)小明先到达终点.(2)方案一:小明在起点,小莉在起点前6米处,两人同时起跑,同时到达;方案二:小莉在起点,小明在起点后![]() 米处,两人同时起跑,同时到达.
米处,两人同时起跑,同时到达.
【解析】试题分析:(1)首先得出两人之间的速度之间关系,进而利用小明从起点向后退6m,得出两人的速度差,求出即可;
(2)利用两人的速度关系得出符合题意的方案.
试题解析:(1)根据题意,得![]() ,则y=
,则y= ![]() .
.
因为![]() ,
,
所以![]()
所以小明先到达终点.
(2)方案一:小明在起点,小莉在起点前6米处,两人同时起跑,同时到达;
方案二:设小莉在起点,小明在起点后a米处,两人同时起跑,同时到达.
则![]() ,
,
即![]() ,
,
解得a=![]() .
.
所以小莉在起点,小明在起点后![]() 米处,两人同时起跑,同时到达.
米处,两人同时起跑,同时到达.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).(参考数据:sin27°≈0.45,cos27°≈0.90,tan27°≈0.50,
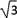 ≈1.73)
≈1.73)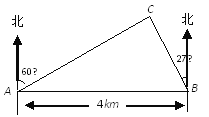
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的长方体,已知它的长为4cm,宽为3cm,高为5cm

(1)求此长方体所有棱长的和;
(2)若它是一个无上盖的精致包装盒,制作这种包装盒的纸每平方厘米是0.1元,问制作10个这样的包装盒共需多少元?(不考虑接缝之间的材料)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是⊙O的直径,AB为⊙O 的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,梯形ABCD中,AD∥BC,∠C=90°,BA=BC.动点E、F同时从点B出发,点E沿折线 BA–AD–DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.
请根据图中的信息,解答下列问题:
(1)AD= cm,BC= cm;
(2)求a的值,并用文字说明点N所表示的实际意义;
(3)直接写出当自变量t为何值时,函数y的值等于5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AD平分
中,AD平分 交BC于点D,F为AD上一点,且
交BC于点D,F为AD上一点,且 ,BF的延长线交AC于点E.
,BF的延长线交AC于点E.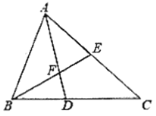

备用图
(1)求证:
 ;
;(2)若
 ,
, ,
, ,求DF的长;
,求DF的长; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线的流水线上依次有5个机器人,它们站立的位置在数轴上依次用点A、B、C、D、E表示

(1)点B与点E之间的距离是多少?
(2)怎样移动点C,使它先到达点B,再到达点E?用文字说明
(3)若原点是零件供应点,则5个机器人分別到达供应点的路程之和是多少?
相关试题

