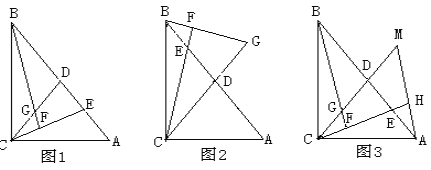
【题目】已知:在△ABC中,AC=BC, ![]() ,过点C作CD⊥AB于点D,点E是AB边上一动点(不同于点A、B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G(如图1).
,过点C作CD⊥AB于点D,点E是AB边上一动点(不同于点A、B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G(如图1).
(1)求证:BG=CE;
(2)若点E运动到线段BD上时(如图2),试猜想BG、CE的数量关系是否发生变化?请直接写出你的结论;
(3)过点A作AH垂直于直线CE垂足为点H并交CD的延长线于点M(如图3),找出图中与BE相等的线段,并证明.
参考答案:
【答案】(1)证明见解析;(2)不变,BG=CE;(3)BE=CM,理由见解析.
【解析】试题分析:(1)先由等边对等角得出∠ABC=∠CAB,再由同角的余角相等证得∠ACE=∠CBG,再由等腰直角三角形的性质得出∠A=∠BCD,由边角边可得△BCG≌△ACE,即可证得BG=CE;
(2)如图②,根据等腰直角三角形的性质可以得出∠BCD=∠ACD=45°,根据直角三角形的三角形的性质就可以得出∠CBF=∠ACE,由ASA就可以得出BCG≌△ACE,就可以得出结论;
(3)如图③,根据等腰直角三角形的性质可以得出∠BCD=∠ACD=45°,根据直角三角形的三角形的性质就可以得出∠BCE=∠CAM,由ASA就可以得出△BCE≌△CAM,就可以得出结论;
证明:(1) ∵AC=BC,
∴∠ABC=∠CAB,
∵∠ACB=90°,
∴∠ABC=∠A=45°,∠ACE+∠BCE=90°,
∵BF⊥CE,
∴∠BFC=90°,
∴∠CBG+∠BCE=90°,
∴∠ACE=∠CBG,
∵在Rt△ABC中,CD⊥AB,AC=BC,
∴∠BCD=∠ACD=45°,
∴∠A=∠BCD,
在△BCG和△CAE中,
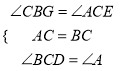 ,
,
∴△BCG≌△ACE(ASA),
∴BG=CE;
(2)不变.BG=CE;
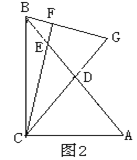
∵AC=BC,
∴∠ABC=∠CAB,
∵∠ACB=90°,
∴∠ABC=∠A=45°,∠ACE+∠BCE=90°,
∵BF⊥CE,
∴∠BFC=90°,
∴∠CBG+∠BCE=90°,
∴∠ACE=∠CBG,
∵在Rt△ABC中,CD⊥AB,AC=BC,
∴∠BCD=∠ACD=45°,
∴∠A=∠BCD,
在△BCG和△CAE中,
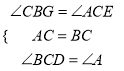 ,
,
∴△BCG≌△ACE(ASA),
∴BG=CE;
(3)BE=CM,
理由:∵AC=BC,∠ACB=90°,
∴∠ABC=∠CAB=45°,∠ACE+∠BCE=90°,
∵AH⊥CE,
∴∠AHC=90°,
∴∠HAC+∠ACE=90°,
∴∠BCE=∠HAC,
即:∠BCE=∠CAM,
∵在RT△ABC中,CD⊥AB,AC=BC,
∴∠BCD=∠ACD=45°
∴∠ACD=∠ABC,
即:∠ACM=∠CBE,
在△BCE和△CAM中, 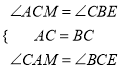 ,
,
∴△BCE≌△CAM(ASA)
∴BE=CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+y2=10,xy=2,则(x+y)2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解
(1)2a2﹣8
(2)x2(x﹣2)+4(2﹣x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:如图①,直线
 直线
直线 ,垂足为
,垂足为 ,点
,点 在射线
在射线 上,点
上,点 在射线
在射线 上(
上( 、
、 不与
不与 点重合),点
点重合),点 在射线
在射线 上且
上且 ,过点
,过点 作直线
作直线 .点
.点 在点
在点 的左边且
的左边且

(1)直接写出的
 面积 ;
面积 ;(2)如图②,若
 ,作
,作 的平分线交
的平分线交 于
于 ,交
,交 于
于 ,试说明
,试说明 ;
;

(3)如图③,若
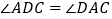 ,点
,点 在射线
在射线 上运动,
上运动, 的平分线交
的平分线交 的延长线于点
的延长线于点 ,在点
,在点 运动过程中
运动过程中 的值是否变化?若不变,求出其值;若变化,求出变化范围.
的值是否变化?若不变,求出其值;若变化,求出变化范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的横坐标为( )

A. 44 B. 45 C. 46 D. 47
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、D、C、F在一条直线上,且BD=FC,AB=EF.

(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中,装有3个分别写有数字6,﹣2,7的小球,他们的形状、大小、质地完全相同,搅拌均匀后,先从盒子里随机抽取1个小球,记下小球上的数字后放回盒子,搅拌均匀后再随机取出1个小球,再记下小球上的数字.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出所有可能出现的结果;
(2)求两次取出的小球上的数字相同的概率P.
相关试题

