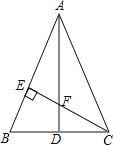
【题目】如图,△ABC中,AB=AC,作AD⊥BC,CE⊥AB,垂足分别为D,E,AD和CE相交于点F,若已知AE=CE.
(1)求证:△AEF≌△CEB;
(2)求证:AF=2CD
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)要证明△AEF≌△CEB,已知条件有AE=EC,∠AEF=∠BEC=90°,还差一个条件,由AD⊥BC,CE⊥AB可得∠B+∠BAD=90°,∠B+∠BCE=90°,所以得出∠EAF=∠ECB,因此可证明出△AEF≌△CEB;(2)由(1)结论可得:AF=BC,即要证明BC=2CD,由等腰三角形三线合一性质不难证明.
试题解析:
(1)证明:∵AD⊥BC,
∴∠B+∠BAD=90°,
∵CE⊥AB,
∴∠B+∠BCE=90°,
∴∠EAF=∠ECB,
在△AEF和△CEB中,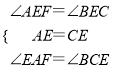 ,
,
∴△AEF≌△CEB;
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC,
∴CD=BD,BC=2CD,
∴AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将550000用科学记数法表示是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于-2且小于3的所有整数的和为_________.
-
科目: 来源: 题型:
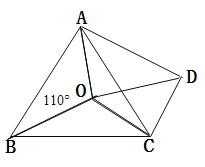
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a,以OC为一边作等边△OCD,连接AD.
(1)求证:△BOC≌△ADC;
(2)当OA=OD时,求a的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,过点D作DF⊥BC,垂足为F,DF与AC交于点M,已知∠1=∠2.
(1)求证:CM=DM;
(2)若FB=FC,求证:AM-MD=2FM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂设计了一款工艺品,每件成本
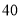 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是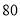 元时,每天的销售量是
元时,每天的销售量是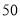 件,若销售单价每降低
件,若销售单价每降低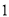 元,每天就可多售出
元,每天就可多售出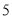 件,但要求销售单价不得低于
件,但要求销售单价不得低于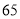 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利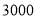 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元?
相关试题

