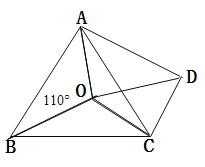
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a,以OC为一边作等边△OCD,连接AD.
(1)求证:△BOC≌△ADC;
(2)当OA=OD时,求a的值
参考答案:
【答案】(1)证明见解析;(2)110°.
【解析】试题分析:(1)要证明△BOC≌△ADC,已知条件有AC=BC,CO=CD,
试题解析:
(1)∵△ABC是等边三角形,△COD是等边三角形,
∴BC=AC,CO=CD,∠ACB=∠OCD=60°,
∴∠BCO=∠ACD,
在△BOC和△ADC中,
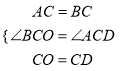 ,
,
∴△BOC≌△ADC;
(2)当OA=OD时,∠OAD=∠ODA,
∠OAD=∠DAC+∠OAC=∠OBC+∠OAC=360°-∠AOC-∠BOC-∠ACO-∠BCO=110°-60°=50°,
∴∠ODA=50°,
∴∠BOC=∠ADC=50°+60°=110°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将550000用科学记数法表示是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于-2且小于3的所有整数的和为_________.
-
科目: 来源: 题型:
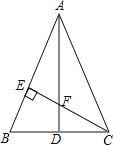
查看答案和解析>>【题目】如图,△ABC中,AB=AC,作AD⊥BC,CE⊥AB,垂足分别为D,E,AD和CE相交于点F,若已知AE=CE.
(1)求证:△AEF≌△CEB;
(2)求证:AF=2CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,过点D作DF⊥BC,垂足为F,DF与AC交于点M,已知∠1=∠2.
(1)求证:CM=DM;
(2)若FB=FC,求证:AM-MD=2FM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂设计了一款工艺品,每件成本
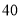 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是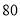 元时,每天的销售量是
元时,每天的销售量是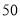 件,若销售单价每降低
件,若销售单价每降低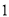 元,每天就可多售出
元,每天就可多售出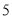 件,但要求销售单价不得低于
件,但要求销售单价不得低于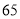 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利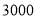 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)射线AB与射线BA是同一条射线;(2)两点之间,直线最短;(3)在
 ,(﹣3)3 , ﹣22 , 0,﹣(﹣2)中,负数的个数有3个;(4)若AP=PB,则点P是线段AB的中点;(5)一条直线的平行线有且只有一条.其中错误的个数为( )
,(﹣3)3 , ﹣22 , 0,﹣(﹣2)中,负数的个数有3个;(4)若AP=PB,则点P是线段AB的中点;(5)一条直线的平行线有且只有一条.其中错误的个数为( )A. 2 B. 3 C. 4 D. 5
相关试题

