【题目】定向越野作为一种新兴的运动项目,深受人们的喜爱. 这种定向运动是利用地图和指北针到访地图上所指示的各个点标,以最短时间按序到达所有点标者为胜. 下面是我区某校进行定向越野活动中,中年男子组的成绩(单位:分:秒).
9:01 14:45 9:46 19:22 11:20 18:47 11:40 12:32 11:52 13:45
22:27 15:00 17:30 13:22 18:34 10:45 19:24 16:26 21:33 15:31
19:50 14:27 15:55 16:07 20:43 12:13 21:41 14:57 11:39 12:45
12:57 15:31 13:20 14:50 14:57 9:41 12:13 14:27 12:25 12:38
例如,用时最少的赵老师的成绩为9:01,表示赵老师的成绩为9分1秒.

以下是根据某校进行定向越野活动中,中年男子组的成绩中的数据,绘制的统计图表的一部分.
某校中年男子定向越野成绩分段统计表
分组/分 | 频数 | 频率 |
9≤x<11 | 4 | 0.1 |
11≤x<13 | b | 0.275 |
13≤x<15 | 9 | 0.225 |
15≤x<17 | 6 | d |
17≤x<19 | 3 | 0.075 |
19≤x<21 | 4 | 0.1 |
21≤x<23 | 3 | 0.075 |
合计 | a | c |
(1)这组数据的极差是____________;
(2)上表中的a =____________ ,b =____________ , c =____________, d =____________;
(3)补全频数分布直方图.
参考答案:
【答案】见解析
【解析】
(1)先找出这组成绩的最大值与最小值,计算即可得;
(2)根据分组“9≤x<11”的频数与频率可求得a的值,然后用a乘0.275可求得b的值,用6除以a可得d,把所有频率相加可求得c,据此填空即可;
(3)根据b的值补全图形即可.
(1)这组数据的最大值为22:27,最小值为9:01,
所以极差为:22:27-9:01=13:26,
故答案为:13:26或 13分26秒;
(2)a=4÷0.1=40,b=40×0.275=11,d=6÷40=0.15,
c=0.1+0.275+0.225+0.15+0.075+0.1+0.075=1,
故答案为:40,11,1,0.15.
(3)如图所示.
-
科目: 来源: 题型:
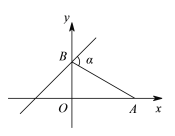
查看答案和解析>>【题目】如图,已知A点的坐标为
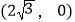 ,直线
,直线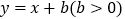 与y轴交于点B,连接AB,若
与y轴交于点B,连接AB,若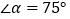 ,则
,则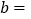 ____________.
____________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点A作已知直线l的平行线”.

小云的作法如下:
(1)在直线l 上任取一点B,以点B为圆心,AB长为半径作弧, 交直线l 于点C;
(2)分别以A,C为圆心,以AB长为半径作弧,两弧相交于点D;
(3)作直线AD.
所以直线AD即为所求.
老师说:“小云的作法正确”.
请回答:小云的作图依据是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:
(1)“基础电价”是____________元
 度;
度;(2)求出当x>240 时,y与x的函数表达式;
(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
 ﹣1的步骤如下:
﹣1的步骤如下:(解析)第一步:
 ﹣1(分数的基本性质)
﹣1(分数的基本性质)第二步:2x﹣1=3(2x+8)﹣3……(①)
第三步:2x﹣1=6x+24﹣3……(②)
第四步:2x﹣6x=24﹣3+1……(③)
第五步:﹣4x=22(④)
第六步:x=﹣
 ……(⑤)
……(⑤)以上解方程第二步到第六步的计算依据有:①去括号法则.②等式性质一.③等式性质二.④合并同类项法则.请选择排序完全正确的一个选项( )
A. ②①③④② B. ②①③④③ C. ③①②④③ D. ③①④②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列方程,属于一元一次方程的有( )
①x﹣2=
 ;②0.5x=1;③
;②0.5x=1;③ =8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
=8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x
…
0.5
1
1.5
2
2.5
3
3.5
…
y
…
1.75
3
3.75
4
3.75
3
m
…
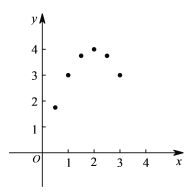
写出m=____________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.
相关试题

