【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,PA=3,PB=1,CD=PC=2,CD⊥PC.
(1)找出图中一对全等三角形,并证明;
(2)求∠BPC的度数.

参考答案:
【答案】(1)△APC≌△BDC,理由见解析;(2) ∠BPC=135°.
【解析】
(1)根据同角的余角相等求出∠ACP=∠BCD,再利用“边角边”证明△APC≌△BDC;
(2)先判断出△PCD是等腰直角三角形,再根据全等三角形对应边相等可得AP=BD,然后利用勾股定理逆定理判断出△BPD是直角三角形,∠BPD=90°,再根据∠BPC=∠BPD+∠CPD代入数据计算即可得解
(1)△APC≌△BDC,理由如下:
∵∠ACB=90°,CD⊥CP,∴∠ACB=∠PCD,
∴∠ACB-∠PCB=∠PCD-∠PCB,
即∠ACP=∠BCD,
又∵AC=BC,PC=DC,∴△APC≌△BDC(SAS).
(2)∵△APC≌△BDC,∴AP=BD,
∵PC=CD=2,∠PCD=90°,
∴PD2=PC2+CD2=8,∠CPD=45°.
∵PA=3,PB=1,∴BD=3,∴BD2=9,PB2=1.
∴BD2=PB2+PD2,∴∠BPD=90°.
∴∠BPC=∠BPD+∠CPD=135°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.
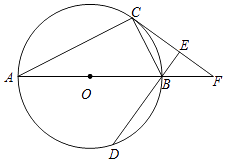
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为时,四边形ACFD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.
(1)求AC的长;(2)求ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:
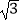 .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,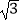 ≈1.73.)
≈1.73.)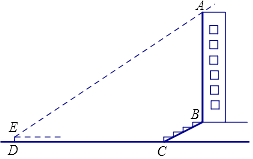
相关试题

