【题目】某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1: ![]() .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.73.)
≈1.73.)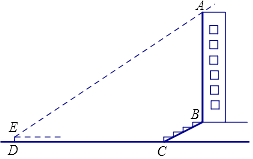
参考答案:
【答案】解:.
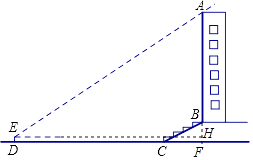
∵在Rt△BCF中, ![]() =i=1:
=i=1: ![]() ,
,
∴设BF=k,则CF= ![]() ,BC=2k.
,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF= ![]() .
.
∵DF=DC+CF,
∴DF=40+6 ![]() .
.
∵在Rt△AEH中,tan∠AEH= ![]() ,
,
∴AH=tan37°×(40+6 ![]() )≈37.785(米),
)≈37.785(米),
∵BH=BF﹣FH,
∴BH=6﹣1.5=4.5.
∵AB=AH﹣HB,
∴AB=37.785﹣4.5≈33.3.
答:大楼AB的高度约为33.3米.
【解析】根据已知条件,添加辅助线,延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,由BC得坡度和BC得长,求出BF,CF的长,即可求得DF的长,再在在Rt△AEH中,根据解直角三角形,求得AH、BH的长,从而可求得大楼AB的高度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,PA=3,PB=1,CD=PC=2,CD⊥PC.
(1)找出图中一对全等三角形,并证明;
(2)求∠BPC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AO∶BO=2∶3.
(1)求AC的长;(2)求ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=
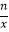 的图象交于C、D两点,已知点C的坐标为(﹣4,﹣1),点D的横坐标为2.
的图象交于C、D两点,已知点C的坐标为(﹣4,﹣1),点D的横坐标为2.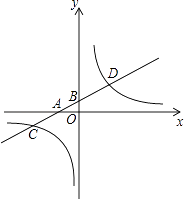
(1)求反比例函数与一次函数的解析式;
(2)直接写出当x为何值时,y1>y2?
(3)点P是反比例函数在第一象限的图象上的点,且点P的横坐标大于2,过点P做x轴的垂线,垂足为点E,当△APE的面积为3时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,气象部门观测到距A市正南方向240km的B处有一台风中心,其中心最大风力为12级,该台风中心正以20km/h的速度沿北偏东30°的BC方向移动,且台风中心风力不变,已知每远离台风中心20km,风力就减弱一级,台风中心在移动的过程中,其周围130km的范围内都要受到影响.
(1)A市是否会受到这次台风影响?若受台风影响,则所受的最大风力是几级?
(2)A市遭受到这次台风影响多长时间?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市决定购买A、B两种树苗对某段道路进行绿化改造,已知购买A种树苗9棵,B种树苗4棵,需要700元;购买A种树苗3棵,B种树苗5棵,则需要380元.
(1)求购买A、B两种树苗每颗各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于60棵,且用于购买这两种树苗的资金不能超过5260元.若购进这两种树苗共100棵,则有哪几种购买方案?哪种方案最省钱?
相关试题

