搜索
【题目】如图，网格中的每个小正方形的边长为1，A，B是格点，则以A，B，C为等腰三角形顶点的所有格点C的位置有（ ）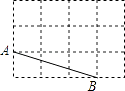
A.2个
B.3个
C.4个
D.5个
参考答案：
【答案】C
【解析】解：由勾股定理得：AB= 
= 
，
分三种情况：如图所示：
①当A为顶角顶点时，符合△ABC为等腰三角形的C点有1个；
②当B为顶角顶点时，符合△ABC为等腰三角形的C点有2个；
③当C为顶角顶点时，符合△ABC为等腰三角形的C点有1个；
综上所述：以A，B，C为等腰三角形顶点的所有格点C的位置有1+2+1=4（个）；
故选：C．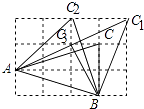
先利用勾股定理求出AB的长，然后分三种情况：①当A为顶角顶点时；②当B为顶角顶点时；③当C为顶角顶点时，分别求出符合△ABC为等腰三角形的个数，即可得出答案。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点B．C．D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H．
①△BCE≌△ACD；
②CF=CH；
③△CFH为等边三角形；
④FH∥BD；
⑤AD与BE的夹角为60°，
以上结论正确的是 ．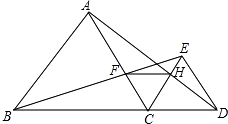
-
科目： 来源： 题型：
查看答案和解析>>【题目】化简求值。
（1）已知x+y=15，x2+y2=113，求x2﹣xy+y2的值．
（2）先化简，再求值：
÷ 
+1，在0，1，2，三个数中选一个合适的，代入求值． -
科目： 来源： 题型：
查看答案和解析>>【题目】一个长方形的周长是（6a+8b），其中一边长为（2a+3b),求另一边长.
-
科目： 来源： 题型：
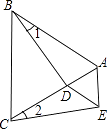
查看答案和解析>>【题目】如图，△ABC是等边三角形，D是AC上一点，BD=CE，∠1=∠2，试判断BC与AE的位置关系，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某通讯公司推出①、②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间的函数关系如图所示．
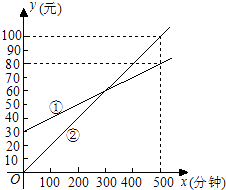
（1）有月租费的收费方式是（填①或②），月租费是元；
（2）分别求出①、②两种收费方式中y与自变量x之间的函数关系式；
（3）请你根据用户通讯时间的多少，给出经济实惠的选择建议． -
科目： 来源： 题型：
查看答案和解析>>【题目】下面事件是随机事件的是（ ）
A.掷一枚硬币，出现反面
B.在标准大气压下，水加热到8℃时会沸腾
C.实数的绝对值不小于零
D.如果a，b是实数，那么ab＝ba
相关试题
