【题目】某河流受暴雨影响,水位不断上涨,下面是某天此河流的水位记录:
时间(时) | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
水位(米) | 2 | 2.5 | 3 | 4 | 5 | 6 | 8 |
(1)上表反映的是哪两个量之间的关系?自变量和因变量各是什么?
(2)根据表格画了表示两个变量的折线统计图.
(3)哪段时间水位上升得最快?
参考答案:
【答案】(1)时间和水位之间的关系,时间是自变量,水位是因变量;(2)见解析;(3)20-24水位上升最快.
【解析】
(1)根据表格可知是时间和水位之间的关系,在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中水位随时间的变化记录画图;
(3)相同的时间上升的水位越多代表上升的越快,根据此规律看表数据即可判断.
解:(1)根据表格可知是时间和水位之间的关系,并且每过4个小时水位在变化,可知水位随着时间在变化,即时间是自变量,水位是因变量;
(2)见下图:
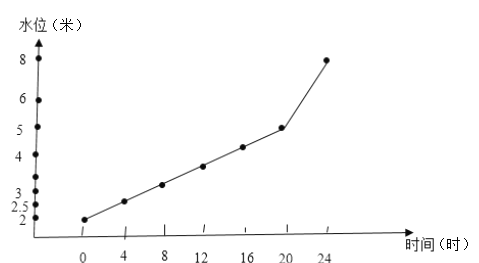
(3)0-4时的变化情况为2.5-2=0.5m;
4-8时的变化情况为3-2.5=0.5m;
8-12时的变化情况为4-3=1m;
12-16时的变化情况为5-4=1m;
16-20时的变化情况为6-5=1m;
20-24时的变化情况为8-6=2m;
∴20-24水位上升最快.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆每年夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
(1)什么情况下,购会员证与不购证付一样的钱?
(2)什么情况下,购会员证比不购证更合算?
(3)什么情况下,不购会员证比购证更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一边靠墙,其他三边用12米长的篱笆围成一个矩形(ABCD)花圃.

(1)如果设花圃靠墙的一边的长为x(米).花圃的面积为y(平方米),求x,y满足的关系式;
(2)当长x从4米变到6米时,面积y变化如何?
(3)当长x从6米变到8米时,面积y变化如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点
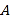 、点
、点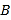 表示的数分别为
表示的数分别为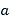 、
、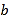 ,则
,则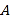 、
、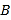 两点之间的距离
两点之间的距离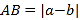 ,线段
,线段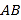 的中点表示的数为
的中点表示的数为 .
.(问题情境)
如图,数轴上点
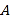 表示的数为
表示的数为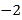 ,点
,点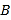 表示的数为8,点
表示的数为8,点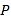 从点
从点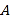 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点 从点
从点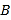 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为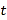 秒(
秒(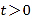 ).
).(综合运用)
(1)填空:
①
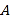 、
、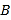 两点之间的距离
两点之间的距离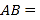 ________,线段
________,线段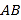 的中点表示的数为__________.
的中点表示的数为__________.②用含
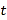 的代数式表示:
的代数式表示: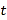 秒后,点
秒后,点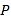 表示的数为____________;点
表示的数为____________;点 表示的数为___________.
表示的数为___________.③当
 _________时,
_________时,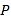 、
、 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.(2)当
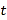 为何值时,
为何值时,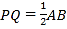 .
.(3)若点
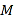 为
为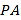 的中点,点
的中点,点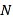 为
为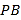 的中点,点
的中点,点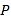 在运动过程中,线段
在运动过程中,线段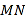 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段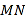 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的方法拼成一个边长为(m+n)的正方形.
⑴ 请用两种不同的方法求图2中阴影部分的面积.
方法1: ;方法2: ;
⑵ 观察图2写出
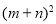 ,
,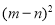 ,
,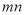 三个代数式之间的等量关系: ;
三个代数式之间的等量关系: ;⑶ 根据⑵中你发现的等量关系,解决如下问题:若
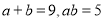 ,求
,求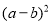 的值.
的值.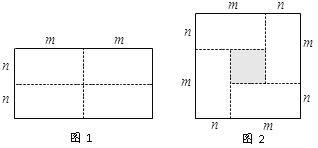
-
科目: 来源: 题型:
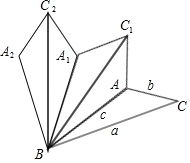
查看答案和解析>>【题目】在△ABC中,∠ABC<20°,三边长分别为a,b,c,将△ABC沿直线BA翻折,得到△ABC1;然后将△ABC1沿直线BC1翻折,得到△A1BC1;再将△A1BC1沿直线A1B翻折,得到△A1BC2;…,若翻折4次后,得到图形A2BCAC1A1C2的周长为a+c+5b,则翻折11次后,所得图形的周长为_____________.(结果用含有a,b,c的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:
 ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.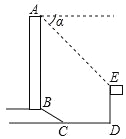
相关试题

