【题目】在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆” 
(1)已知点P的坐标为(2,0) ①若点Q的坐标为(0,1),求点P、Q的“相关圆”的面积;
②若点Q的坐标为(3,n),且点P、Q的“相关圆”的半径为 ![]() ,求n的值;
,求n的值;
(2)已知△ABC为等边三角形,点A和点B的坐标分别为(﹣ ![]() ,0)、(
,0)、( ![]() ,0),点C在y轴正半轴上,若点P、Q的“相关圆”恰好是△ABC的内切圆且点Q在直线y=2x上,求点Q的坐标.
,0),点C在y轴正半轴上,若点P、Q的“相关圆”恰好是△ABC的内切圆且点Q在直线y=2x上,求点Q的坐标.
(3)已知△ABC三个顶点的坐标为:A(﹣3,0)、B( ![]() ,0),C(0,4),点P的坐标为(0,
,0),C(0,4),点P的坐标为(0, ![]() ),点Q的坐标为(m,
),点Q的坐标为(m, ![]() ),若点P、Q的“相关圆”与△ABC的三边中至少一边存在公共点,直接写出m的取值范围.
),若点P、Q的“相关圆”与△ABC的三边中至少一边存在公共点,直接写出m的取值范围.
参考答案:
【答案】
(1)解:①∵PQ= ![]() =
= ![]() =
= ![]() ,
,
∴S=πr2=5π.
②过点Q作QH⊥x轴于H.

∵HQ= ![]() =2,
=2,
∴Q点坐标为(3,2)或(3,﹣2).
∴n=2或﹣2
(2)解:如图,
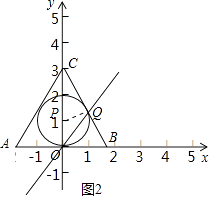
在Rt△OAC中,∠ACO=30°,
∴OC= ![]() OA=3,
OA=3,
∴C点坐标为(0,3),
∴△ABC的内切圆的圆心的坐标为(0,1),半径为1,
∴P(0,1),
设Q(x,2x),则有x2+(2x﹣1)2=1,
解得x= ![]() ,
,
∴Q( ![]() ,
, ![]() )
)
(3)解:如图3中,

①当相关圆与AC、AB相切时半径有最小值 ![]() .
.
②当相关圆经过点B时,半径有最大值 ![]() ,
,
∴﹣ ![]() ≤m≤﹣
≤m≤﹣ ![]() ,
, ![]() ≤m≤
≤m≤ ![]()
【解析】(1)①根据PQ= ![]() =
= ![]() =
= ![]() ,求出⊙P的半径即可解决问题;②过点Q作QH⊥x轴于H.利用勾股定理求出QH的值,即可解决问题;(2)在Rt△OAC中,∠ACO=30°,可得OC=
,求出⊙P的半径即可解决问题;②过点Q作QH⊥x轴于H.利用勾股定理求出QH的值,即可解决问题;(2)在Rt△OAC中,∠ACO=30°,可得OC= ![]() OA=3,推出C点坐标为(0,3),推出△ABC的内切圆的圆心的坐标为(0,1),半径为1,推出P(0,1),设Q(x,2x),则有x2+(2x﹣1)2=1,求出x即可;(3)①当相关圆与AC、AB相切时,可得半径有最小值
OA=3,推出C点坐标为(0,3),推出△ABC的内切圆的圆心的坐标为(0,1),半径为1,推出P(0,1),设Q(x,2x),则有x2+(2x﹣1)2=1,求出x即可;(3)①当相关圆与AC、AB相切时,可得半径有最小值 ![]() .②当相关圆经过点B时,可得半径最大值
.②当相关圆经过点B时,可得半径最大值 ![]() ,由此即可解决问题;
,由此即可解决问题;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )
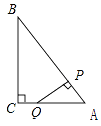
A.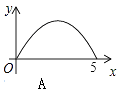
B.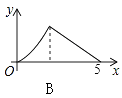
C.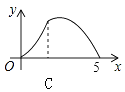
D.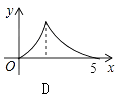
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①同位角相等;
②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;
③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;
④同一平面内两条直线的位置关系可能是平行或垂直;
⑤有公共顶点并且相等的角是对顶角.
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为( )
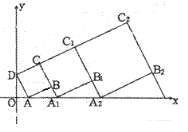
A.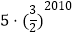
B.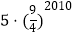
C.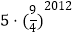
D.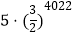
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
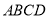 中,边
中,边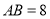 ,
,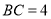 ,以点
,以点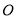 为原点,
为原点,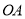 ,
,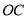 所在的直线为
所在的直线为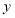 轴和
轴和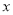 轴,建立直角坐标系.
轴,建立直角坐标系.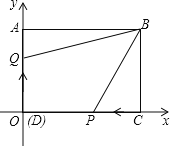
(1)点
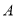 的坐标为
的坐标为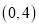 ,则
,则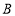 点坐标为______,
点坐标为______,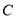 点坐标为______;
点坐标为______;(2)当点
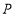 从
从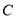 出发,以2单位/秒的速度沿
出发,以2单位/秒的速度沿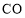 方向移动(不过
方向移动(不过 点),
点), 从原点
从原点 出发以1单位/秒的速度沿
出发以1单位/秒的速度沿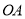 方向移动(不过
方向移动(不过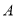 点),
点),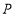 ,
,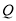 同时出发,在移动过程中,四边形
同时出发,在移动过程中,四边形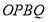 的面积是否变化?若不变,求其值;若变化,求其变化范围.
的面积是否变化?若不变,求其值;若变化,求其变化范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD的长为( )

A. 2 B. 3 C. 4 D. 2
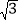
相关试题

