搜索
【题目】下列说法正确的有（ ）
①同位角相等；
②若∠A+∠B+∠C＝180°，则∠A、∠B、∠C互补；
③同一平面内的三条直线a、b、c，若a∥b，c与a相交，则c与b相交；
④同一平面内两条直线的位置关系可能是平行或垂直；
⑤有公共顶点并且相等的角是对顶角．
A. 1个B. 2个C. 3个D. 4个
参考答案：
【答案】A
【解析】
根据相交直线的位置关系综合判定即可.
解：∵同位角不一定相等，∴①错误；
∵互补或互余是两个角之间的关系，∴说∠A+∠B+∠C＝180°，则∠A、∠B、∠C互补错误，∴②错误；
∵同一平面内的三条直线a、b、c，若a∥b，c与a相交，则c与b相交，∴③正确；
∵同一平面内两条直线的位置关系可能是平行或相交，∴④错误；
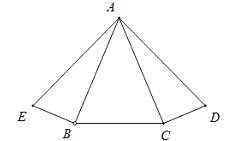
∵如图，
∠ABC＝∠ABD，∠ABC和∠ABD有公共顶点并且相等的角，但不是对顶角，∴⑤错误；
即正确的个数是1个，
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店分两次购进
、
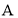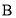两种商品进行销售，两次购进同一种商品的进价相同，具体情况如下表所示：购进数量（件）
购进所需费用（元）
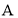
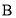
第一次
30
40
3800
第二次
40
30
3200
（1）求
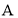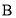、两种商品每件的进价分别是多少元？（2）商场决定
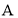种商品以每件30元出售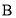，种商品以每件100元出售．为满足市场需求，需购进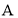、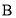两种商品共1000件，且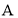种商品的数量不少于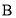种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠ABE=∠ACD=Rt∠，AE=AD，∠ABC=∠ACB.求证：∠BAE=∠CAD．
请补全证明过程，并在括号里写上理由．
证明：在△ABC中，
∵∠ABC=∠ACB
∴AB= （ ）
在Rt△ABE和Rt△ACD中，
∵ =AC， =AD
∴Rt△ABE≌Rt△ACD（ ）
∴∠BAE=∠CAD（ ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC中，∠C=90°，AC=3，BC=4，P是斜边AB上一动点（不与点A、B重合），PQ⊥AB交△ABC的直角边于点Q，设AP为x，△APQ的面积为y，则下列图象中，能表示y关于x的函数关系的图象大致是（ ）
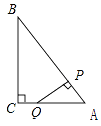
A.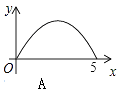
B.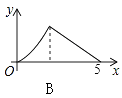
C.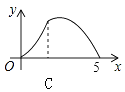
D.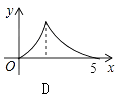
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠BAC＝90°，AD＝CD，点E是边AC的中点，连接DE，DE的延长线与边BC相交于点F，AG∥BC，交DE于点G，连接AF、CG.
(1)求证：AF＝BF；
(2)如果AB＝AC，求证：四边形AFCG是正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，点P与点Q不重合，以点P为圆心作经过Q的圆，则称该圆为点P、Q的“相关圆”
（1）已知点P的坐标为（2，0） ①若点Q的坐标为（0，1），求点P、Q的“相关圆”的面积；
②若点Q的坐标为（3，n），且点P、Q的“相关圆”的半径为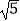
，求n的值；
（2）已知△ABC为等边三角形，点A和点B的坐标分别为（﹣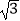
，0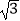）、（ ，0），点C在y轴正半轴上，若点P、Q的“相关圆”恰好是△ABC的内切圆且点Q在直线y=2x上，求点Q的坐标．
（3）已知△ABC三个顶点的坐标为：A（﹣3，0）、B（
，0），C（0，4），点P的坐标为（0， 
），点Q的坐标为（m， ），若点P、Q的“相关圆”与△ABC的三边中至少一边存在公共点，直接写出m的取值范围． -
科目： 来源： 题型：
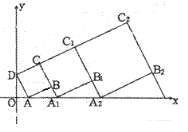
查看答案和解析>>【题目】在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1 ， 作正方形A1B1C1C，延长C1B1交x轴于点A2 ， 作正方形A2B2C2C1,………按这样的规律进行下去，第2012个正方形的面积为（ ）
A.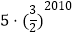
B.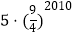
C.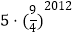
D.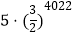
相关试题
