【题目】某通讯公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80分钟通话时间,超过80分钟的部分,以每分钟0.15元的价格计费.
下列结论:
①如图描述的是方式1的收费方法;
②若月通话时间少于240分钟,选择方式2省钱;
③若月通讯费为50元,则方式1比方式2的通话时间多;
④若方式1比方式2的通讯费多10元,则方式1比方式2的通话时间多100分钟.
其中正确的是( )
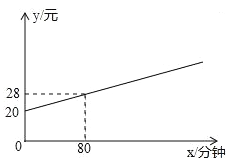
A.只有①② B.只有③④ C.只有①②③ D.①②③④
参考答案:
【答案】C.
【解析】
试题解析:根据题意得:
方式一的函数解析式为y=0.1x+20,
方式二的函数解析式为y=![]() ,
,
①方式一的函数解析式是一条直线,方式二的函数解析式是分段函数,所以如图描述的是方式1的收费方法,另外,当x=80时,方式一是28元,方式二是20元,故①说法正确;
②0.1x+20>20+0.15×(x-80),解得x<240,故②的说法正确;
③当y=50元时,方式一:0.1x+20=50,解得x=300分钟,方式二:20+0.15×(x-80)=50,解得x=280分钟,故③说法正确;
④如果方式一通话费用为40元
则方式一通话时间为:![]() =200,方式二通讯时间为:
=200,方式二通讯时间为:![]() ≈147
≈147
因此若方式1比方式2的通讯费多10元,则方式1比方式2的通话时间多53分钟,故④说法错误;
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个直七棱柱,它的底面边长都是
 ,侧棱长是
,侧棱长是 ,观察这个棱柱,请回答下列问题:
,观察这个棱柱,请回答下列问题: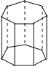
 这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出
这个七棱柱共有多少个面,它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想出 棱柱有多少个面?
棱柱有多少个面? 这个七棱柱一共有多少条棱?它们的长度分别是多少?
这个七棱柱一共有多少条棱?它们的长度分别是多少? 这个七棱柱一共有多少个顶点?
这个七棱柱一共有多少个顶点? 通过对棱柱的观察,你能说出
通过对棱柱的观察,你能说出 棱柱的顶点数与
棱柱的顶点数与 的关系及棱的条数与
的关系及棱的条数与 的关系吗?
的关系吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C.

(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在一次函数
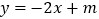 的图象上,它们的横坐标依次为
的图象上,它们的横坐标依次为 ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A. 1 B. 3 C.
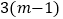 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
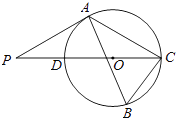
(1)求证:PA是⊙O的切线;
(2)若AB=4+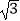 ,BC=2
,BC=2 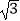 ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,画一个长和宽分别为
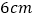 、
、 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.
 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体? 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4= ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标,观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集
相关试题

