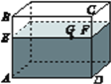
【题目】有一个如图所示的长方体的透明鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵.
(1)小虫应该走怎样的路线才可使爬行的路程最短?请画出它的爬行路线,并用箭头标注;
(2)试求小虫爬行的最短路程.
参考答案:
【答案】(1)如图所示见解析,AQ→QG为最短路线;(2)小虫爬行的最短路程为100 cm.
【解析】
(1)根据轴对称性质,通过作对称点将折线转化成两点之间线段距离最短.
(2)根据AE=40cm,AA′=120cm,可得:A′E=120-40=80(cm),再根据EG=60cm,可得:A′G2=A′E2+EG2=802+602=10000,A′G=100cm,进而可得:AQ+QG=A′Q+QG=A′G=100cm.
(1)如图所示,AQ→QG为最短路线,

(2)因为AE=40cm,AA′=120cm,所以A′E=120-40=80(cm),
因为EG=60cm,所以A′G2=A′E2+EG2=802+602=10000,
所以A′G=100cm,所以AQ+QG=A′Q+QG=A′G=100cm,
所以小虫爬行的最短路程为100cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河边有A,B两个村庄,A村距河边10 m,B村距河边30 m,两村平行于河边方向的水平距离为30 m,现要在河边建一抽水站,需铺设管道抽水到A村和B村.
(1)求铺设管道的最短长度是多少,请画图说明;
(2)若铺设管道每米需要500元,则最低费用为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.
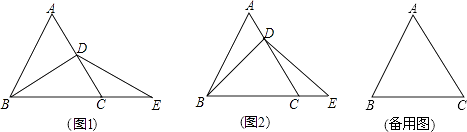
(1)若点D是AC的中点,如图1,求证:AD=CE.
(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC,交AB于点F.)
(3)若点D在线段AC的延长线上,(2)中的结论是否仍成立?如果成立,给予证明;如果不成立,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+c分别交x轴于A(4,0)、B(﹣1,0),交y轴于点C(0,﹣3),过点A的直线y=﹣
 x+3交抛物线于另一点D.
x+3交抛物线于另一点D.
(1)求抛物线的解析式及点D的坐标;
(2)若点P位x轴上的一个动点,点Q在线段AC上,且Q到x轴的距离为 ,连接PC、PQ,当△PCQ的周长最小时,求出点P的坐标;
,连接PC、PQ,当△PCQ的周长最小时,求出点P的坐标;
(3)如图2,在(2)的结论下,连接PD,在平面内是否存在△A1P1D1 , 使△A1P1D1≌△APD(点A1、P1、D1的对应点分别是A、P、D,A1P1平行于y轴,点P1在点A1上方),且△A1P1D1的两个顶点恰好落在抛物线上?若存在,请求出点A1的横坐标m,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在由6个边长为1的小正方形组成的方格中:
(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是2002年北京第24届国际数学家大会会徽,由4个全等的直角三角形拼合而成,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么(a+b)2的值为( )

A.13
B.19
C.25
D.169 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )

A.75°
B.60°
C.54°
D.67.5°
相关试题

