【题目】如图,在边长为2 ![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.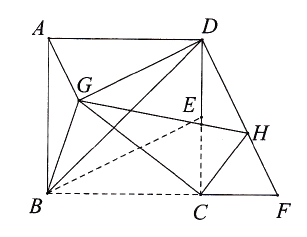
参考答案:
【答案】2
【解析】解:如图,过C作CK⊥DF于K,过H作HM⊥CF于M,过G作PN⊥BC,交AD于P,交BC于N,
∵CD=2 ![]() ,CE=CF=
,CE=CF= ![]() ,
,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴∠DCF=90°,
由勾股定理得:DF= ![]() ,
,
∵CK⊥DF,DC⊥CF,
∴∠FCK=∠CDF,
sin∠FCK=sin∠CDF= ![]() ,
,
∴ ![]() ,
,
∴FK=1,
∴CK= ![]() ,
,
由旋转得:CH=CE=CF,
∵CK⊥FH,
∴HF=2KF,
∴HF=2,
∴S△CHF= ![]() CFHM=
CFHM= ![]() HFCK,
HFCK,![]() HM=2×2,
HM=2×2,
HM= ![]() ,
,
∴CM= ![]() ,
,
∴tan∠HCF=  ,
,
设HM=4x,CM=3x,则CH=5x,
∵∠HCF=∠GCD=∠CGN,
∴cos∠CGN=cos∠HCF= ![]() =
= ![]() ,
,
∴GN= ![]() CG,
CG,
∵CG=BC=2 ![]() ,
,
∴GN= ![]() ×2
×2 ![]() =
= ![]() ,
,
∴NC= ![]() =
= ![]() ,
,
∴GP=2 ![]() -
- ![]() =
= ![]() ,
,
∴AP=BN=BC-NC=2 ![]() -
- ![]() =
= ![]() ,
,
由勾股定理得:AG= ![]()
![]() .
.
所以答案是:2.
【考点精析】本题主要考查了勾股定理的概念的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算机系统对文件的管理通常采用树形目录结构,方式如图,在一个根目录下建立若干子目录(这里称第一层目录),每个子目录又可作为父目录,向下继续建立其子目录(这里称第二层目录),依次进行,可创建多层目录.现在一根目录下建立了四层目录,并且每一个父目录下的子目录的个数都相同,都等于根目录下目录的个数.已知第三层目录共有343个,求这一根目录下的所有目录的个数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l分别交x轴、y轴于点A、B,交曲线y=
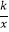 (x>0)于点C,若AB:AC=1:3,且S△AOB=
(x>0)于点C,若AB:AC=1:3,且S△AOB= 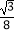 ,则k的值为( )
,则k的值为( )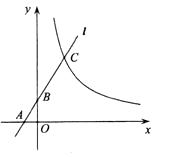
A.
B.2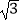
C.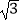
D.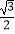
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于
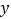 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简分式:
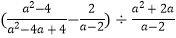 ,再从不等式组
,再从不等式组 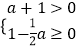 的解集中选出合适的整数作为a的值,代入求值.
的解集中选出合适的整数作为a的值,代入求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图信息,L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象,问

(1)在刚出发时我公安快艇距走私船多少海里?
(2)计算走私船与公安快艇的速度分别是多少?
(3)写出L1,L2的解析式
(4)问6分钟时两艇相距几海里.
(5)猜想,公安快艇能否追上走私船,若能追上,那么在几分钟追上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在直角坐标系中,A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1)
(1)继续填写A5(______);A6(______);A7(______):A8(______);A9(______);A10(______);A11(______)
(2)依据上述规律,写出点A2017,A2018的坐标.

相关试题

