【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字﹣1、0、2,它们除了数字不同外,其他都完全相同.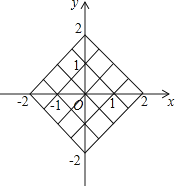
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为;
(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的纵坐标,请用树状图或表格列出点M所有可能的坐标,并求出点M落在如图所示的正方形网格内(包括边界)的概率.
参考答案:
【答案】
(1)![]()
(2)
解:画树状图为:
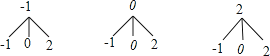
共有9种等可能的结果数,其中点M落在如图所示的正方形网格内(包括边界)的结果数为6,
所以点M落在如图所示的正方形网格内(包括边界)的概率= ![]() =
= ![]()
【解析】解:(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率= ![]() ; 所以答案是
; 所以答案是 ![]() ;
;
【考点精析】掌握列表法与树状图法和概率公式是解答本题的根本,需要知道当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知A(a,0),B (0,b)分别为两坐标轴上的点,且a,b满足a2﹣24a+|b﹣12|=﹣144,且3OC=OA.
(1)求A、B、C三点的坐标;
(2)若D(2,0),过点D的直线分别交AB、BC于E、F两点,且DF=DE,设E、F两点的横坐标分别为xE、xP,求xE+xP的值;
(3)如图2,若M(4,8),点P是x轴上A点右侧一动点,AH⊥PM于点H,在HM上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否改变?若不变,请求其值;若改变,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是 .
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是 .
(3)如果锐锐将每道题各用一次“求助”,请用树状图或者列表来分析他顺序通关的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目
学生长跑
短跑
跳绳
跳远
200
√
×
√
√
300
×
√
×
√
150
√
√
√
×
200
√
×
√
×
150
√
×
×
×
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大? -
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t≤1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生数为人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把横纵坐标都是整数的点称为“整点”.

(1)直接写出函数y=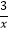 图象上的所有“整点”A1 , A2 , A3 , …的坐标;
图象上的所有“整点”A1 , A2 , A3 , …的坐标;
(2)在(1)的所有整点中任取两点,用树状图或列表法求出这两点关于原点对称的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的平均数,中位数分别是( )
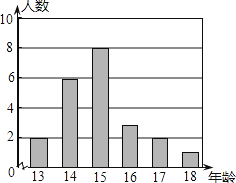
A.15.5,15.5
B.15.5,15
C.15,15.5
D.15,15
相关试题

