【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的
的
图像交于点A.
(1)求点A的坐标;
(2)在y轴上确定点M,使得△AOM是等腰三角形,请直接写出点M的坐标;
(3)如图,设x轴上一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△ABC的面积及点B、点C的坐标;
OA,求△ABC的面积及点B、点C的坐标;
(4)在(3)的条件下,设直线![]() 交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.
交x轴于点D,在直线BC上确定点E,使得△ADE的周长最小,请直接写出点E的坐标.

参考答案:
【答案】(1)(3,4); (2)点M为(0,5)、(0,﹣5)、(0,8)、(0,![]() );(3)点B(9,12)、C(9,﹣2);(4)点E坐标为(9,1).
);(3)点B(9,12)、C(9,﹣2);(4)点E坐标为(9,1).
【解析】
试题(1)联立方程组,求解.(2)分类讨论在y轴上确定点OM= OA,OM=AM,总共有4种可能性.(3) 设点B(a,![]() a),C(a,﹣a+7),利用BC=
a),C(a,﹣a+7),利用BC=![]() OA,求a值.过点A作AQ⊥BC,求得△ABC的面积及点B、点C的坐标.(4)利用对称求最小值.
OA,求a值.过点A作AQ⊥BC,求得△ABC的面积及点B、点C的坐标.(4)利用对称求最小值.
试题解析:
解:(1)联立得: ,解得:
,解得:![]() ,
,
则点A的坐标为(3,4).
(2)根据勾股定理得:OA=![]() =5,
=5,
如图1所示,

分四种情况考虑:
当OM1=OA=5时,M1(0,5);
当OM2=OA=5时,M2(0,﹣5);
当AM3=OA=5时,M3(0,8);
当OM4=AM4时,M4(0,![]() ),
),
综上,点M为(0,5)、(0,﹣5)、(0,8)、(0,![]() );
);
(3)设点B(a,![]() a),C(a,﹣a+7),
a),C(a,﹣a+7),
∵BC=![]() OA=
OA=![]() ×5=14,
×5=14,
∴![]() a﹣(﹣a+7)=14,
a﹣(﹣a+7)=14,
解得:a=9,
过点A作AQ⊥BC,如图2所示,

∴S△ABC=![]() BCAQ=
BCAQ=![]() ×14×(9﹣
×14×(9﹣
当a=9时,![]() a=
a=![]() ×9=12,﹣a+7=﹣9+7=﹣2,
×9=12,﹣a+7=﹣9+7=﹣2,
∴点B(9,12)、C(9,﹣2).
(4)如图3所示,

作出D关于直线BC的对称点D′,连接AD′,与直线BC交于点E,连接DE,此时△ADE周长最小,
对于直线y=﹣x+7,令y=0,得到x=7,即D(7,0),
由(3)得到直线BC为直线x=9,
∴D′(11,0),
设直线AD′解析式为y=kx+b,
把A与D′坐标代入得:![]() ,
,
解得: ,
,
∴直线AD′解析式为y=﹣![]() x+
x+![]() ,
,
令x=9,得到y=1,
则此时点E坐标为(9,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)自2014年12月启动“绿茵行动,青春聚力”郴州共青林植树活动以来,某单位筹集7000元购买了桂花树和樱花树共30棵,其中购买桂花树花费3000元.已知桂花树比樱花树的单价高50%,求樱花树的单价及棵树.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+2的图象与反比例函数y=﹣
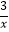 的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称. 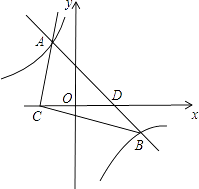
(1)求A、B两点的坐标;
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等.

(1)求x的值.
(2)求正方体的上面和底面的数字和.
相关试题

