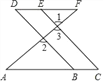
【题目】已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.
解:∵∠1=∠2 (已知 )
∠1=∠ ( )
∴∠2=∠ (等量代换)
∴BD∥ ( )
∴∠ABD=∠ (两直线平行,同位角相等)
∵∠A=∠F ( 已知 )
∴DF∥ ( )
∴∠ABD=∠ (两直线平行,内错角相等)
∴∠C=∠D ( ).
参考答案:
【答案】3;对顶角相等;3;EC;同位角相等,两直线平行;C;AC;内错角相等,两直线平行;D;等量代换
【解析】试题分析:根据平行线的判定方法:同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行做题求解.
试题解析:∵∠1=∠2(已知),
∠2=∠3(对顶角相等),
∴∠1=∠3(等量代换),
∴BD∥EC(同位角相等,两直线平行 ),
∴∠ABD=∠C(两直线平行,同位角相等),
∵∠A=∠F(已知),
∴DF∥AC(内错角相等,两直线平行),
∴∠ABD=∠D(两直线平行,内错角相等 ),
∴∠C=∠D(等量代换).
故答案为:3;对顶角相等;3;EC;同位角相等,两直线平行;C;AC;内错角相等,两直线平行;D;等量代换
-
科目: 来源: 题型:
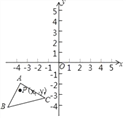
查看答案和解析>>【题目】如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)
(1)请写出三角形ABC平移的过程;
(2)写出点A′,C′的坐标;
(3)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,点
,点 在
在 上,点
上,点 在
在 的内部,
的内部,  平分
平分 ,且
,且 .
.(1)求证:
 ;
;(2)求证:点
 是线段
是线段 的中点.
的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题12分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
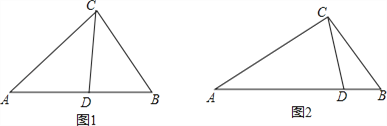
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=
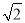 ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组数据为边长,能构成三角形的是( )
A.4, 4, 9B.4, 5, 9C.3, 10, 4D.3, 6, 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的3倍,这个角的度数是( )
A.30°B.45°C.60°D.75°
相关试题

