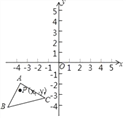
【题目】如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)
(1)请写出三角形ABC平移的过程;
(2)写出点A′,C′的坐标;
(3)求△A′B′C′的面积.
参考答案:
【答案】(1)见解析;(2)A′(2,3),C′(5,1);(3)5.5
【解析】试题分析:(1),根据△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),结合“左减右加,上加下减”的平移规律可完成解答;
(2),根据所得的图形,结合象限内点的坐标特征可完成解答;
(3),用长方形的面积减去三个直角三角形的面积,即可求出△A′B′C′的面积.
试题解析:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
(2)由(1)可知,A′(2,3),C′(5,1);
(3)如图所示,S△A′B′C′=3×4﹣![]() ×1×3﹣
×1×3﹣![]() ×1×4﹣
×1×4﹣![]() ×2×3=5.5.
×2×3=5.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,正确的是()
A.9ab-3ab=6B.3a+4b= 7abC.x2y-2 y x2= -x2yD.a4+a6=a10
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图某幢大楼顶部有广告牌CD.张老师目高MA为1.60米,他站立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进14米、站在点B处,测得广告牌顶端点C的仰角为45°.(取
 ,计算结果保留一位小数)
,计算结果保留一位小数)
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018南1月24日是腊八节,这天哈尔滨市的最低气温是﹣35℃,最高气温是﹣24℃,这一天哈尔滨市的温差为( )
A. 9℃ B. 10℃ C. 11℃ D. 59℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,点
,点 在
在 上,点
上,点 在
在 的内部,
的内部,  平分
平分 ,且
,且 .
.(1)求证:
 ;
;(2)求证:点
 是线段
是线段 的中点.
的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

-
科目: 来源: 题型:
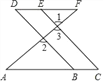
查看答案和解析>>【题目】已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.
解:∵∠1=∠2 (已知 )
∠1=∠ ( )
∴∠2=∠ (等量代换)
∴BD∥ ( )
∴∠ABD=∠ (两直线平行,同位角相等)
∵∠A=∠F ( 已知 )
∴DF∥ ( )
∴∠ABD=∠ (两直线平行,内错角相等)
∴∠C=∠D ( ).
相关试题

