【题目】(本题12分)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
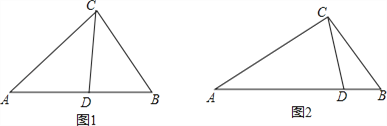
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
参考答案:
【答案】(1)答案见解析;(2)96°或114°;(3)![]()
【解析】试题分析:(1)根据完美分割线的定义只要证明①△ABC不是等腰三角形,②△ACD是等腰三角形,③△BDC∽△BCA即可.
(2)分三种情形讨论即可①如图2,当AD=CD时,②如图3中,当AD=AC时,③如图4中,当AC=CD时,分别求出∠ACB即可.
(3)设BD=x,利用△BCD∽△BAC,得![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
(1)如图1中,∵∠A=40°,∠B=60°,∴∠ACB=80°,∴△ABC不是等腰三角形,∵CD平分∠ACB,∴∠ACD=∠BCD=![]() ∠ACB=40°,∴∠ACD=∠A=40°,∴△ACD为等腰三角形,∵∠DCB=∠A=40°,∠CBD=∠ABC,∴△BCD∽△BAC,∴CD是△ABC的完美分割线.
∠ACB=40°,∴∠ACD=∠A=40°,∴△ACD为等腰三角形,∵∠DCB=∠A=40°,∠CBD=∠ABC,∴△BCD∽△BAC,∴CD是△ABC的完美分割线.
(2)①当AD=CD时,如图2,∠ACD=∠A=45°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=96°.
②当AD=AC时,如图3中,∠ACD=∠ADC=(180°-48°)÷2=66°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∴∠ACB=∠ACD+∠BCD=114°.
③当AC=CD时,如图4中,∠ADC=∠A=48°,∵△BDC∽△BCA,∴∠BCD=∠A=48°,∵∠ADC>∠BCD,矛盾,舍弃,∴∠ACB=96°或114°.
(3)由已知AC=AD=2,∵△BCD∽△BAC,∴ ![]() 设BD=x,∴
设BD=x,∴![]() ),∵x>0,∴x=
),∵x>0,∴x=![]() ,∵△BCD∽△BAC,∴
,∵△BCD∽△BAC,∴![]() =
=![]() ,∴CD=
,∴CD=![]() ×2=
×2=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,点
,点 在
在 上,点
上,点 在
在 的内部,
的内部,  平分
平分 ,且
,且 .
.(1)求证:
 ;
;(2)求证:点
 是线段
是线段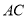 的中点.
的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

-
科目: 来源: 题型:
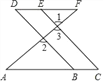
查看答案和解析>>【题目】已知:如图,∠1=∠2,∠A=∠F,试说明∠C=∠D.
解:∵∠1=∠2 (已知 )
∠1=∠ ( )
∴∠2=∠ (等量代换)
∴BD∥ ( )
∴∠ABD=∠ (两直线平行,同位角相等)
∵∠A=∠F ( 已知 )
∴DF∥ ( )
∴∠ABD=∠ (两直线平行,内错角相等)
∴∠C=∠D ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组数据为边长,能构成三角形的是( )
A.4, 4, 9B.4, 5, 9C.3, 10, 4D.3, 6, 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角的补角是它的余角的3倍,这个角的度数是( )
A.30°B.45°C.60°D.75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,直接写出∠A和∠C之间的数量关系________;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.

相关试题

