搜索
【题目】在一个木箱中装有卡片共50张，这些卡片共有三种，它们分别标有1、2、3的字样，除此之外其他都相同，其中标有数字2的卡片的张数是标有数字3卡片的张数的3倍少8张．已知从箱子中随机摸出一张标有数字1卡片的概率是 
．
（1）求木箱中装有标1的卡片张数；
（2）求从箱子中随机摸出一张标有数字3的卡片的概率．
参考答案：
【答案】
（1）解：根据题意得：
50× 
=10，
答：箱中装有标1的卡片10张；
（2）解：设装有标3的卡片x张，则标2的卡片有3x﹣8张，
根据题意得：x+3x﹣8=40，
解得：x=12，
所以摸出一张有标3的卡片的概率P= 
= 
．
【解析】（1）用总数乘以标有数字1的概率即可求得张数；（2）首先列方程求得标3的卡片的张数，然后利用概率公式求解即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算下列各题
（1）
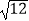﹣3tan30°+（4﹣π）0﹣（ 
）﹣1
（2）先化简，再求值：（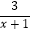
﹣x+1）÷ 
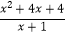，其中x= 
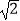﹣2． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图，射线CB∥OA，∠C=∠OAB=100°，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF。
（1）求∠EOB的度数；
（2）若平行移动AB，那么∠OBC∶∠OFC的值是否随之变化？若变化，找出变化规律；若不变，求出这个比值；
（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=∠OBA？若存在，求出其度数；若不存在，说明理由。
-
科目： 来源： 题型：
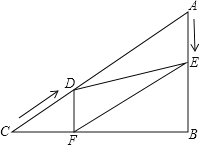
查看答案和解析>>【题目】如图所示，在Rt△ABC中，∠B=90°，AC=100cm，∠A=60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤25）．过点D作DF⊥BC于点F，连接DE，EF．
（1）求证：四边形AEFD是平行四边形；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①所示，已知，BC∥OA，∠B=∠A=100°，试解答下列问题：
（1）试说明：OB∥AC；
（2）如图②，若点E．F在BC上，且∠FOC=∠AOC，OE平分∠BOF.试求∠EOC的度数；
（3）在（2）小题的条件下，若左右平行移动AC，如图③，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值.
（4）在（3）小题的条件下，当∠OEB=∠OCA时，试求∠OCA的度数.
-
科目： 来源： 题型：
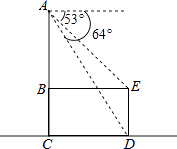
查看答案和解析>>【题目】如图是放在水平地面上的一把椅子的侧面图，椅子高为AC，椅面宽为BE，椅脚高为ED，且AC⊥BE，AC⊥CD，AC∥ED．从点A测得点D、E的俯角分别为64°和53°．已知ED=35cm，求椅子高AC约为多少？
（参考数据：tan53°≈
，sin53°≈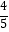 
，tan64°≈2，sin64°≈ 
）
-
科目： 来源： 题型：
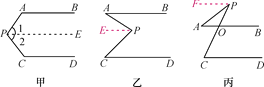
查看答案和解析>>【题目】阅读下列解答过程：（1）如图甲，AB∥CD，探索∠P与∠A，∠C之间的关系．
（2）如图乙和图丙，AB∥CD，请根据上述方法分别探索两图中∠P与∠A，∠C之间的关系．
相关试题
