【题目】已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
A.点O在△ABC的三边垂直平分线上
B.点O在△ABC的三个内角平分线上
C.如果△ABC的面积为S,三边长为a,b,c,⊙O的半径为r,那么r=![]()
D.如果△ABC的三边长分别为5,7,8,那么以A、B、C为端点三条切线长分别为5,3,2
参考答案:
【答案】A
【解析】解:∵⊙O是△ABC的内切圆,
∴点O到△ABC三边的距离相等,
∴点O在△ABC的三个内角平分线上,故A错误,B正确,
连接OA,OB,OC,
∴S=S△ABO+S△BCO+S△ACO=![]() cr+
cr+![]() ar
ar![]() br=
br=![]() (a+b+c)r,
(a+b+c)r,
∴r=![]() , 故C正确,
, 故C正确,
设以A、B、C为端点三条切线长分别为:x,y,z,
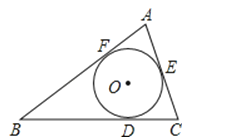
则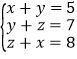 ,
,
解得:![]() ,
,
故D正确,
故选A.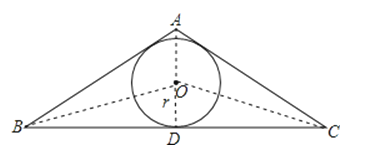
【考点精析】认真审题,首先需要了解三角形的内切圆与内心(三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l上有三个正方形a,b,c,若a,c的面积分别为2和10,则b的面积为( )

A. 8 B.
 C.
C.  D. 12
D. 12 -
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( )
A.AF=4,BD=9,CE=5
B.AF=4,BD=5,CE=9
C.AF=5,BD=4,CE=9
D.AF=9,BD=4,CE=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若AD∥BC,AB∥DE,DF∥AC,∠OEC=72°,∠OCE=64°,则∠B=_______,∠F=_______,∠BAD=_______,∠ADF=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
-
科目: 来源: 题型:
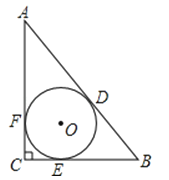
查看答案和解析>>【题目】如图,⊙O为△ABC的内切圆,D、E、F分别为切点,已知∠C=90°,⊙O半径长为3cm,AC=10cm,则AD长度为cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=
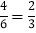 .
.(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=
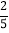 .
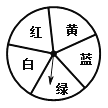
.(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=
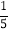 .
.问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

相关试题

