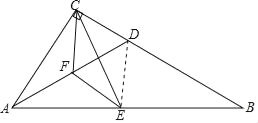
【题目】如图,Rt△ABC中,∠ACB=90°,D是边BC上一点,点E、F分别是线段AB、AD中点,联结CE、CF、EF.
(1)求证:△CEF≌△AEF;
(2)联结DE,当BD=2CD时,求证:AD=2DE.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)在直角三角形ABC中,E为斜边AB的中点,利用斜边上的中线等于斜边的一半得到CE=AE,在直角三角形ACD中,F为斜边AD的中点,利用斜边上的中线等于斜边的一半得到AF=CF,再由EF=EF,利用SSS即可得证;
(2)由EF为三角形ABD的中点,利用中位线定理得到EF与BD平行,EF等于BD的一半,再由BD=2DC,等量代换得到EF=CD,再由EF与CD平行,得到四边形CEFD为平行四边形,可得出DE=CF,再由CF=AF,等量代换得到DE=AF.
证明:(1)∵∠ACB=90°,且E线段AB中点,
∴CE=![]() AB=AE,
AB=AE,
∵∠ACD=90°,F为线段AD中点,
∴AF=CF=![]() AD,
AD,
在△CEF和△AEF中,
 ,
,
∴△CEF≌△AEF(SSS);
(2)连接DE,
∵点E、F分别是线段AB、AD中点,
∴EF=![]() BD,EF∥BC,
BD,EF∥BC,
∵BD=2CD,
∴EF=CD.
又∵EF∥BC,
∴四边形CFEDD是平行四边形,
∴DE=CF,
∵CF=AF=FD,
∴AD=2DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型物件快递公司送货员每月的工资由底薪加计件工资两部分组成,计件工资与送货件数成正比例.有甲乙两名送货员,如果送货量为x件时,甲的工资是y1(元),乙的工资是y2(元),如图所示,已知甲的每月底薪是800元,每送一件货物,甲所得的工资比乙高2元
(1)根据图中信息,分别求出y1和y2关于x的函数解析式;(不必写定义域)
(2)如果甲、乙两人平均每天送货量分别是12件和14件,求两人的月工资分别是多少元?(一个月为30天)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从仓库O出发在东西街道上运送水果,规定向东为正方向,一次到达的5个销售地点依次分别为A,B,C,D,E,最后回到仓库O,货车行驶的记录(单位:千米)如下:+1,+3,﹣6,﹣1,﹣2,+5.请问:
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,E的位置;
(2)试求出该货车共行驶了多少千米?
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记为负数,则运往A,B,C,D,E五个地点的水果重量可记为:
+50,﹣15,+25,﹣10,﹣15,则该货车运送的水果总重量是多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造铁力旅游景点,市旅游局打算将依吉密河中一段长1800米的河道整治任务交由甲、乙两个工程队来完成.已知,甲工程队每天整治60米,乙工程队每天整治40米.
(1)若甲、乙两个工程队接龙来完成,共用时35天,求甲、乙两个工程队分别整治多长的河道?
(2)若乙工程队先整治河道10天,甲工程队再参加两个工程队一起来完成剩余河道整治任务,求整段河道整治任务共用时多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用长度相等的小棒按一定规律摆成的一组图案.
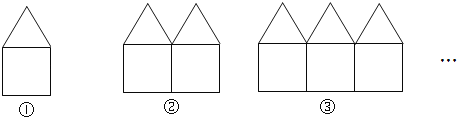
(1)第1个图案中有6根小棒;第2个图案中有 根小棒;第3个图案中有 根小棒;
(2)第n个图案中有多少根小棒?
(3)第25个图案中有多少根小棒?
(4)是否存在某个符合上述规律的图案,由2032根小棒摆成?如果有,指出是滴几个图案;如果没有,请说明理由.
-
科目: 来源: 题型:
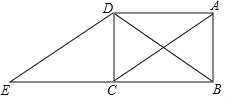
查看答案和解析>>【题目】如图,在矩形ABCD中,连接对角线AC、BD,将△ABC沿BC方向平移,使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC;
(2)请探究△BDE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标平面内,直线y=﹣
 x﹣4与x轴、y轴分别交于点A、B,点C在x轴正半轴上,且满足OC=
x﹣4与x轴、y轴分别交于点A、B,点C在x轴正半轴上,且满足OC= OB.
OB.(1)求线段AB的长及点C的坐标;
(2)设线段BC的中点为E,如果梯形AECD的顶点D在y轴上,CE是底边,求点D的坐标和梯形AECD的面积.

相关试题

