【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6![]() ,则另一直角边BC的长为 .
,则另一直角边BC的长为 .

参考答案:
【答案】7.
【解析】
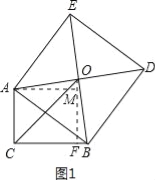
试题分析:过O作OF垂直于BC,再过A作AM垂直于OF,由四边形ABDE为正方形,得到OA=OB,∠AOB为直角,可得出两个角互余,再由AM垂直于MO,得到△AOM为直角三角形,其两个锐角互余,利用同角的余角相等可得出一对角相等,再由一对直角相等,OA=OB,利用AAS可得出△AOM与△BOF全等,由全等三角形的对应边相等可得出AM=OF,OM=FB,由三个角为直角的四边形为矩形得到ACFM为矩形,根据矩形的对边相等可得出AC=MF,AM=CF,等量代换可得出CF=OF,即△COF为等腰直角三角形,由斜边OC的长,利用勾股定理求出OF与CF的长,根据OF﹣MF求出OM的长,即为FB的长,由CF+FB即可求出BC的长.解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF中,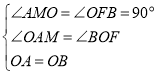 ,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6
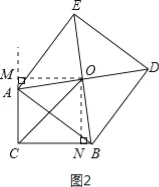
,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6![]() ,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6
,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6![]() ,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.
,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为 :P,即P=|x|+|y|(其中“+”是四则运算中的加法).
(1)求点A(-1,3),B(
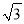 +2,
+2, 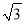 -2)的勾股值A、B;
-2)的勾股值A、B;(2)求满足条件N=3的所有点N围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:|﹣
 |+(π﹣3)0+(
|+(π﹣3)0+( )﹣1﹣2cos45°
)﹣1﹣2cos45°(2)解不等式组
 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
-
科目: 来源: 题型:
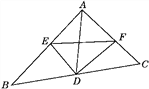
查看答案和解析>>【题目】如图,△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE,DF分别交AB,AC于E,F,且BE2+CF2=EF2,求证:△ABC为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
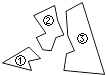
A.带①去
B.带②去
C.带③去
D.带①和②去 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的3个内角之比可以是( )
A. 2:3:4 B. 3:4:5 C. 4:5:6 D. 3:3:6
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x2+1加上一个单项式后,可以分解因式,那么加上的单项式可以是______(只需填写二个).
相关试题

