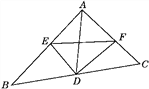
【题目】如图,△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE,DF分别交AB,AC于E,F,且BE2+CF2=EF2,求证:△ABC为直角三角形.
参考答案:
【答案】见解析
【解析】试题分析:延长FD到点M,使DM=DF,连接BM,可证得△CDF≌△BDM,根据全等三角形的性质可得∠DBM=∠C,BM=CF,由∠EDF=90°,MD=FD,根据线段垂直平分线的性质可得EM=EF;再由BE2+CF2=EF2,可得BE2+BM2=EM2,根据勾股定理的逆定理可得△BEM为直角三角形,再证得BM∥AC,由平行线的性质即可证得∠BAC=90°,结论得证.
试题解析:
证明:延长FD至M,使MD=FD,连接MB,ME,如图所示,
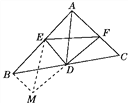
∵D为BC的中点,∴BD=DC,又MD=FD,∠BDM=∠CDF,
∴△BDM≌△CDF(SAS),∴∠DBM=∠C,BM=CF,
∵∠EDF=90°,MD=FD,∴EM=EF,
∵BE2+CF2=EF2,∴BE2+BM2=EM2,
即△BEM为直角三角形,且∠EBM=90°.
由∠DBM=∠C知,BM∥AC,∴∠BAC=180°-∠EBM=90°,
即△ABC为直角三角形.
-
科目: 来源: 题型:
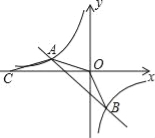
查看答案和解析>>【题目】如图,直线AB与反比例函数的图象交于A(﹣4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.
(1)求反比例函数的解析式.
(2)求cos∠OBA的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为 :P,即P=|x|+|y|(其中“+”是四则运算中的加法).
(1)求点A(-1,3),B(
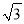 +2,
+2, 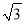 -2)的勾股值A、B;
-2)的勾股值A、B;(2)求满足条件N=3的所有点N围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:|﹣
 |+(π﹣3)0+(
|+(π﹣3)0+( )﹣1﹣2cos45°
)﹣1﹣2cos45°(2)解不等式组
 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
 ,则另一直角边BC的长为 .
,则另一直角边BC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
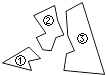
A.带①去
B.带②去
C.带③去
D.带①和②去 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的3个内角之比可以是( )
A. 2:3:4 B. 3:4:5 C. 4:5:6 D. 3:3:6
相关试题

