【题目】在△ABC中,AB=AC,∠BAC=110°,MP、NO分别垂直平分AB、AC.则∠PAO=___________;

参考答案:
【答案】40°.
【解析】
先根据三角形内角和等于180°求出∠B+∠C=70°,再根据线段垂直平分线的性质∠PAB=∠B,∠OAC=∠C,所以∠PAB+∠OAC=70°,再由条件∠BAC=110°就可以求出
∠PAO的度数.
解:∵∠BAC=110°,
∴∠B+∠C=180°-110°=70°,
∵MP,NO为AB,AC的垂直平分线,
∴AP=BP,AO=OC(线段垂直平分线上任意一点,到线段两端点的距离相等),
∴∠BAP=∠B,∠OAC=∠C(等边对等角),
∴∠BAP+∠CAO=70°,
∴∠PAO=∠BAC-∠BAP-∠CAO=110°-70°=40°.
故答案为:40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E分别在钱段AB、AC上,CD与BE交于O,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD

A. ∠B=∠CB. AD=AEC. BE=CDD. BD=CE
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(x―3)2=(3x+1)2 (2)x2-8x=-12
(3)3x2-4x-1=0(用配方法) (4)5x2―7x+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为
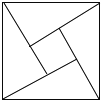
A. 3B. 4C. 5D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD内有一点F,FB与FC分别平分∠ABC和∠BCD,点E为矩形ABCD外一点,连接BE,CE.现添加下列条件:①EB∥CF,CE∥BF;②BE=CE,BE=BF;③BE∥CF,CE⊥BE;④BE=CE,CE∥BF,其中能判定四边形BECF是正方形的共有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足为E,则下列结论:①AD=BF;②∠BAE=∠FBC;③S△ADB=S△ADC;④AC+CD=AB;⑤AD=2BE.其中正确的结论有______(填写序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己如FG⊥AB,、CD⊥AB,垂足分别为G、D,∠1=∠2.
求证:∠CED+∠ACB=180°请将下面的证明过程补充完整.
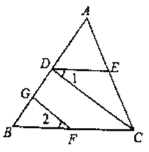
证明:∵FG⊥AB,CD⊥AB(已知),
∴∠FGB=∠CDB=90°(垂直的定义)
∴GF∥CD(___________________________)
∵GF∥CD(已证)
∴∠2=∠BCD(___________________________)
又∵∠1=∠2(已知),
∴∠1=∠BCD(___________________________)
∴___________________________,(___________________________)
∴∠CED+∠ACB=180°(___________________________)
相关试题

