Question

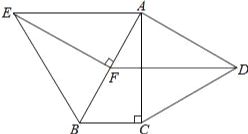
【题目】如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE，已知：∠BAC=30°，EF⊥AB，垂足为F，连接DF．

（1）试说明AC=EF；

（2）求证：四边形ADFE是平行四边形．

Answer 1

【答案】详见解析.

【解析】

试题分析：（1）首先由Rt△ABC中，由∠BAC=30°可以得到AB=2BC，又由△ABE是等边三角形，EF⊥AB，由此得到AE=2AF，并且AB=2AF，然后证得△AFE≌△BCA，继而证得结论；（2）根据（1）知道EF=AC，而△ACD是等边三角形，所以EF=AC=AD，并且AD⊥AB，而EF⊥AB，由此得到EF∥AD，再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形．

试题解析：（1）∵Rt△ABC中，∠BAC=30°，

∴AB=2BC，

又∵△ABE是等边三角形，EF⊥AB，

∴AB=2AF

∴AF=BC，

在Rt△AFE和Rt△BCA中，

，

∴Rt△AFE≌Rt△BCA（HL），

∴AC=EF；

（2）∵△ACD是等边三角形，

∴∠DAC=60°，AC=AD，

∴∠DAB=∠DAC+∠BAC=90°

又∵EF⊥AB，

∴EF∥AD，

∵AC=EF，AC=AD，

∴EF=AD，

∴四边形ADFE是平行四边形．