【题目】在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).

参考答案:
【答案】(1)60°;(2)![]() ;(3)﹣
;(3)﹣![]() ≤m≤
≤m≤![]() .
.
【解析】试题分析:(1)如图1中,根据平行线的性质可得∠AD′C=∠E′CD′=90°,再根据AC=2CD′,推出∠CAD′=30°,由此即可解决问题; (2)如图2中,作CK⊥BE′于K.根据勾股定理和等腰直角三角形的性质求出CK的长,再根据sin∠CBE′= ![]() ,即可解决问题;(3)根据图3、图4分别求出点P横坐标的最大值以及最小值即可解决问题.
,即可解决问题;(3)根据图3、图4分别求出点P横坐标的最大值以及最小值即可解决问题.
试题解析:
(1)如图1中,
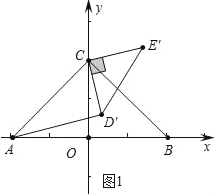
∵AD′∥CE′,
∴∠AD′C=∠E′CD′=90°,
∵AC=2CD′,
∴∠CAD′=30°,
∴∠ACD′=90°﹣∠CAD′=60°,
∴α=60°.
(2)如图2中,作CK⊥BE′于K.
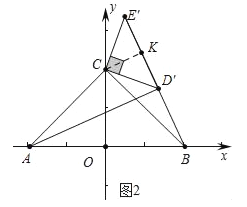
∵AC=BC= ![]() =2
=2 ![]() ,
,
∴CD′=CE′= ![]() ,
,
∵△CD′E′是等腰直角三角形,CD′=CE′= ![]() ,
,
∴D′E′=2,
∵CK⊥D′E′,
∴KD′=E′K,
∴CK= ![]() D′E′=1,
D′E′=1,
∴sin∠CBE′= ![]() =
= ![]() =
= ![]() .
.
(3)如图3中,以C为圆心![]() 为半径作⊙C,当BE′与⊙C相切时AP最长,则四边形CD′PE′是正方形,作PH⊥AB于H.
为半径作⊙C,当BE′与⊙C相切时AP最长,则四边形CD′PE′是正方形,作PH⊥AB于H.
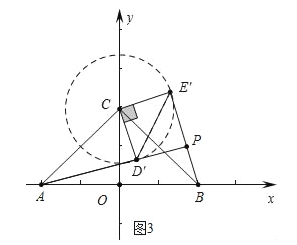
∵AP=AD′+PD′= ![]() +
+ ![]() ,
,
∵cos∠PAB= ![]() =
= ![]() ,
,
∴AH=2+ ![]() ,
,
∴点P横坐标的最大值为![]() .
.
如图4中,当BE′与⊙C相切时AP最短,则四边形CD′PE′是正方形,作PH⊥AB于H.
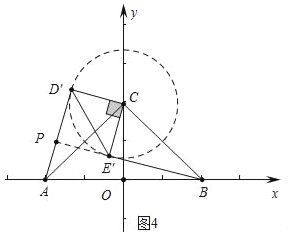
根据对称性可知OH= ![]() ,
,
∴点P横坐标的最小值为﹣![]() ,
,
∴点P横坐标的取值范围为﹣![]() ≤m≤
≤m≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=
 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,求OP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=
 ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称
甲
乙
A
20克
40克
B
30克
20克
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.

(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,D、E是△ABC中BC边上的两点,AD=AE,要证明△ABE≌△ACD,应该再增加一个什么条件?请你增加这个条件后再给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用四块完全相同的小长方形拼成的一个“回形”正方形.

(1)用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式:________;
(2)利用(1)中的结论.计算:
 ,
, ,求
,求 的值;
的值;(3)根据(1)的结论.若
 .求
.求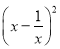 的值.
的值.
相关试题

