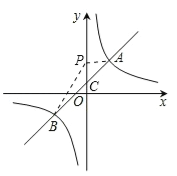
【题目】(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,求OP的长.

参考答案:
【答案】(1)y=x+1;(2)1
【解析】试题分析:(1)将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例函数解析式;设直线AB解析式为y=kx+b,将B坐标代入反比例解析式中求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式;
(2)如图所示,对于一次函数解析式,令x=0求出y的值,确定出C坐标,得到OC的长,三角形ABP面积由三角形ACP面积与三角形BCP面积之和求出,由已知的面积求出PC的长,即可求出OP的长.
解:(1)∵反比例函数y=![]() 的图象经过点A(2,3),
的图象经过点A(2,3),
∴m=6.
∴反比例函数的解析式是y=![]() ,
,
∵B点(﹣3,n)在反比例函数y=![]() 的图象上,
的图象上,
∴n=﹣2,
∴B(﹣3,﹣2),
∵一次函数y=kx+b的图象经过A(2,3)、B(﹣3,﹣2)两点,
∴![]() ,
,
解得:![]() ,
,
∴一次函数的解析式是y=x+1;
(2)对于一次函数y=x+1,令x=0求出y=1,即C(0,1),OC=1,
根据题意得:S△ABP=![]() PC×2+
PC×2+![]() PC×3=5,
PC×3=5,
解得:PC=2,
则OP=OC+CP=1+2=3或OP=CP﹣OC=2﹣1=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC与BD相交于点O,E为BD上的一点,连接EA,将EA绕点E逆时针旋转90°得线段EF,连接FB.

(1)如图a,点E在OB上,
①求∠FEB+∠BAE的度数;
②求证:ED﹣EB=
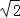 BF;
BF;(2)如图b,当E在OD上时,按已知条件补全图形,直接写出ED、EB、BF三条线段的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣3x2+12x﹣7的顶点坐标为( )
A.(2,5) B.(2,﹣19)
C.(﹣2,5) D.(﹣2,﹣43)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣
 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
-
科目: 来源: 题型:
查看答案和解析>>【题目】由二次函数y=2(x﹣3)2+1可知( )
A.其图象的开口向下
B.其图象的对称轴为x=﹣3
C.其最大值为1
D.当x<3时,y随x的增大而减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中与a-b-c的值不相等的是( )
A. a -(b + c) B. a -(b-c)
C. (a-b)+(-c) D. (-c)-(b-a)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式2x2+3x+7的值为8,则代数式4x2+6x-9的值是( )
A. 13 B. 2 C. 17 D. -7
相关试题

