【题目】(1)(问题解决)已知点![]() 在
在![]() 内,过点
内,过点![]() 分别作关于
分别作关于![]() 、
、![]() 的对称点
的对称点![]() 、
、![]() .
.
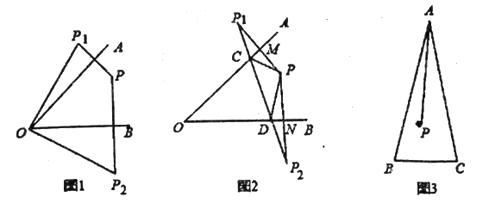
①如图1,若![]() ,请直接写出
,请直接写出![]() ______;
______;
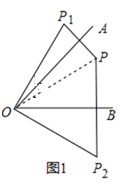
②如图2,连接![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
③在②的条件下,若![]() 度(
度(![]() ),请直接写出
),请直接写出![]() ______度(用含
______度(用含![]() 的代数式表示).
的代数式表示).
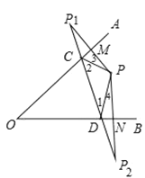
(2)(拓展延伸)利用“有一个角是![]() 的等腰三角形是等边三角形”这个结论,解答问题:如图3,在
的等腰三角形是等边三角形”这个结论,解答问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内部一定点,
内部一定点,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,请你在图3中画出使
上,请你在图3中画出使![]() 周长最小的点
周长最小的点![]() 、
、![]() 的位置(不写画法),并直接写出
的位置(不写画法),并直接写出![]() 周长的最小值.
周长的最小值.
参考答案:
【答案】(1)【问题解决】①![]() ;②
;②![]() ;③
;③![]() ;(2)【拓展延伸】如图,见解析;
;(2)【拓展延伸】如图,见解析;![]() 周长最小值为8.
周长最小值为8.
【解析】
(1)①连接OP,由点P关于直线OA的对称点![]() ,点P关于直线OB的对称点
,点P关于直线OB的对称点![]() ,可得
,可得![]()
![]() ,
,![]()
![]() ,再由
,再由![]()
![]()
![]() +
+![]()
![]() =2(
=2(![]() +
+![]() )=2
)=2![]() ,即可求得∠AOB的度数;②由
,即可求得∠AOB的度数;②由![]() ,根据三角形的内角和定理可得
,根据三角形的内角和定理可得![]() ;由轴对称的性质得,
;由轴对称的性质得,![]() ,
,![]() ,再由三角形外角的性质可得
,再由三角形外角的性质可得![]() ,
,![]() ,所以
,所以![]() ,即可求得
,即可求得![]() ;由轴对称的性质可得
;由轴对称的性质可得![]() ,由四边形的内角和为360°即可求得
,由四边形的内角和为360°即可求得![]() ; ③类比②的方法即可解答;(2)作点P关于边AB的对称点
; ③类比②的方法即可解答;(2)作点P关于边AB的对称点![]() ,再作点P关于边AC的对称点
,再作点P关于边AC的对称点![]() ,连结
,连结![]()
![]() ,分别交AB、AC于点E、F,此时
,分别交AB、AC于点E、F,此时![]() 的周长最小,最小为
的周长最小,最小为![]()
![]() 的长,由①的方法求得∠
的长,由①的方法求得∠![]() A
A![]() =60°,
=60°,![]() A=
A=![]() A,再由“有一个角是
A,再由“有一个角是![]() 的等腰三角形是等边三角形”即可判定△
的等腰三角形是等边三角形”即可判定△![]() A
A![]() 是等边三角形,根据等边三角形的性质可得
是等边三角形,根据等边三角形的性质可得![]()
![]() =AP=8,由此即可得
=AP=8,由此即可得![]() 周长最小值为8.
周长最小值为8.
(1)①连接OP,
∵点P关于直线OA的对称点![]() ,点P关于直线OB的对称点
,点P关于直线OB的对称点![]() ,
,
∴![]()
![]() ,
,![]()
![]() ,
,
∴![]()
![]()
![]() +
+![]()
![]() =2(
=2(![]() +
+![]() )=2
)=2![]() ,
,
故答案为:50°;
②如图2,
∵![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,
∴![]() ;
;
③![]() .
.
如图2,
∵![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由轴对称的性质得,![]() ,
,
∴![]() =
=![]() ;
;
故答案为:![]() ;
;
(2)如图所示,![]() 的周长最小,周长最小值为8.
的周长最小,周长最小值为8.

①画点P关于边AB的对称点![]() ,
,
②画点P关于边AC的对称点![]() ,
,
③连结![]()
![]() ,分别交AB、AC于点E、F,
,分别交AB、AC于点E、F,
此时![]() 的周长最小,周长最小值为8.
的周长最小,周长最小值为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
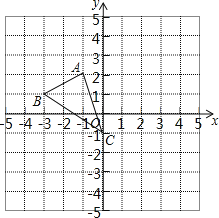
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,直接写出AB与DE的位置关系;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成和对称的格点三角形AFC,直接写出△BCF是什么形状的特殊三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
-
科目: 来源: 题型:
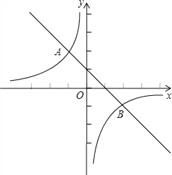
查看答案和解析>>【题目】如图,已知一次函数y=kx+b与反比例函数
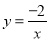 的图象交于A(﹣1,m)、B(n,﹣1)两点.
的图象交于A(﹣1,m)、B(n,﹣1)两点.(1)求出A、B两点的坐标;
(2)求出这个一次函数的表达式;
(3)根据图象,写出使一次函数值大于反比例函数值的x的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
-
科目: 来源: 题型:
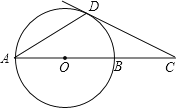
查看答案和解析>>【题目】如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
相关试题

