【题目】如图1,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示.给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=48cm2;③14<t<22时,y=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤当△BPQ与△BEA相似时,t=14.5.其中正确结论的序号是( )

A. ①④⑤ B. ①②④ C. ①③④ D. ①③⑤
参考答案:
【答案】D
【解析】
根据题意,得到P、Q分别同时到达D、C可判断①②,分段讨论PQ位置后可以判断③,再由等腰三角形的分类讨论方法确定④,根据两个点的相对位置判断点P在DC上时,存在△BPQ与△BEA相似的可能性,分类讨论计算即可.
解:由图象可知,点Q到达C时,点P到E则BE=BC=10,ED=4
故①正确
则AE=10﹣4=6
t=10时,△BPQ的面积等于![]()
∴AB=DC=8
故![]()
故②错误
当14<t<22时,![]()
故③正确;
分别以A、B为圆心,AB为半径画圆,将两圆交点连接即为AB垂直平分线
则⊙A、⊙B及AB垂直平分线与点P运行路径的交点是P,满足△ABP是等腰三角形
此时,满足条件的点有4个,故④错误.
∵△BEA为直角三角形
∴只有点P在DC边上时,有△BPQ与△BEA相似
由已知,PQ=22﹣t
∴当![]() 或
或![]() 时,△BPQ与△BEA相似
时,△BPQ与△BEA相似
分别将数值代入
![]() 或
或![]() ,
,
解得t=![]() (舍去)或t=14.5
(舍去)或t=14.5
故⑤正确
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程. 在画函数图象时,我们通过描点、平移、对称的方法画出了所学的函数图象. 同时,我们也学习了绝对值的意义
 ,结合上面经历的学习过程,现在来解决下面的问题
,结合上面经历的学习过程,现在来解决下面的问题在函数
 中,自变量
中,自变量 的取值范围是全体实数,下表是
的取值范围是全体实数,下表是 与
与 的几组对应值:
的几组对应值:

0
1
2
3
y
…
0
1
2
3
2
…
(1)根据表格填写:
 _______.
_______. (2)化简函数解析式:
当
 时,
时, _______;
_______;当
 时,
时, ______.
______.(3)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并解决以下问题;
①该函数的最大值为_______.
②若
 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则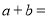 ________.
________.③根据图象可得关于
 的方程
的方程 的解为_______.
的解为_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=
 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,直线
中,直线 与
与 轴、
轴、 轴分别交于点
轴分别交于点 、点
、点 ,直线
,直线 与
与 轴、
轴、 轴分别交于分别交于点
轴分别交于分别交于点 、点
、点 ,直线
,直线 的解析式为
的解析式为 ,直线
,直线 的解析式为
的解析式为 ,两直线交于点
,两直线交于点 ,且
,且 .
. (1)求直线
 的解析式;
的解析式;(2)将直线
 向下平移一定的距离,使得平移后的直线经过
向下平移一定的距离,使得平移后的直线经过 点,且与
点,且与 轴交于点
轴交于点 ,求四边形
,求四边形 的面积.
的面积. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】“唯有书香气,引得大咖来”. 2019年2月14日至15日,由北京师范大学国际写作中心、重庆市第一中学校共同发起的主题为“阅读与写作”——首届“作家进校园”与“校园写作计划”活动隆重举行. 10余位国内文学大咖云集一中校园,开启大师课堂,页再次在校园掀起了读书热潮. 学校图书馆准备购进甲、乙两种书籍若干册供师生阅读,已知购买3册甲种书和4册乙种书共需265元;购买8册甲种书和7册乙种书共需560元.
(1)求甲种、乙种书籍每册各多少元?
(2)学校图书馆计划采购甲、乙两种书籍共710册,沙坪坝新华书店对重庆一中图书馆给予优惠,甲种书的单价不变,而乙种书的单价降价10%,这样购买乙种书的总价仍不低于甲种书的总价,则校图书馆至少需要投入多少资金才能完成采购计划?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正整数
 能表示成
能表示成 (
( 是正整数,且
是正整数,且 )的形式,则称这个数为“明礼崇德数”,
)的形式,则称这个数为“明礼崇德数”, 与
与 是
是 的一个平方差分解. 例如:因为
的一个平方差分解. 例如:因为 ,所以5是“明礼崇德数”,3与2是5的平方差分解;再如:
,所以5是“明礼崇德数”,3与2是5的平方差分解;再如: (
( 是正整数),所以
是正整数),所以 也是“明礼崇德数”,
也是“明礼崇德数”, 与
与 是
是 的一个平方差分解.
的一个平方差分解.(1)判断:9_______“明礼崇德数”(填“是”或“不是”);
(2)已知
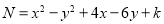 (
( 是正整数,
是正整数, 是常数,且
是常数,且 ),要使
),要使 是“明礼崇德数”,试求出符合条件的一个
是“明礼崇德数”,试求出符合条件的一个 值,并说明理由;
值,并说明理由;(3)对于一个三位数,如果满足十位数字是7,且个位数字比百位数字大7,称这个三位数为“七喜数”.若
 既是“七喜数”,又是“明礼崇德数”,请求出
既是“七喜数”,又是“明礼崇德数”,请求出 的所有平方差分解.
的所有平方差分解. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,以
,以 为边作等腰直角
为边作等腰直角 ,使
,使 ,边
,边 交
交 于点
于点 .
.(1)如图1,过点
 作
作 于点
于点 ,当
,当 时,求线段
时,求线段 的长;
的长;(2)如图2,过点
 作
作 于点
于点 ,且
,且 ,连接
,连接 , 若
, 若 为
为 的中点,求证:
的中点,求证: .
.
相关试题

