【题目】已知:如图, AD=CD=CB=AB=a,DA∥CB,AB⊥CB,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.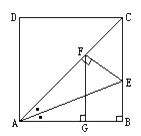
(1)求AC的长;
(2)求证:AB= ![]() AG.
AG.
参考答案:
【答案】
(1)解:∵AB⊥BC
∴∠B=90°
∵AB=BC=a
∴△ABC为等腰直角三角形
∴AC= ![]() =
= ![]() a
a
(2)解:∵△ABC为等腰直角三角形
∴∠CAB=45°
∵FG⊥AB
∴△AFG为等腰直角三角形
∵AE平分∠CAB,EF⊥AC,EB⊥AB
∴△AEF≌△AEB
∴AF=AB=a
∴根据等腰直角△AFG的勾股定理可得:AG= ![]() a ∴AB=
a ∴AB= ![]() AG
AG
【解析】(1)易证△ABC为等腰直角三角形,再由勾股定理可求出AC的长;
(2)由△ABC为等腰直角三角形易证△AFG为等腰直角三角形,从而证明△AEF≌△AEB,则AF=AB=a,再由勾股定理可求出AG的长,进而求出AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差S甲2=1.21,乙的成绩的方差S乙2=3.98,由此可知( ).
A. 甲比乙的成绩稳定 B. 乙比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定 D. 无法确定谁的成绩更稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=
 图象的两个交点.
图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式x3+2x2﹣3的常数项是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种? -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究: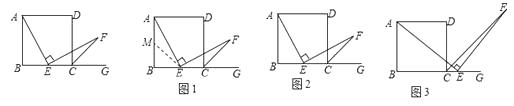
(1)、经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)、小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)、小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由. -
科目: 来源: 题型:
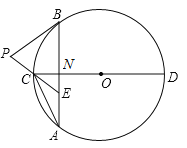
查看答案和解析>>【题目】如图,在⊙O中,直径CD垂直于不过圆心O的弦AB,垂足为点N,连接AC,点E在AB上,且AE=CE.
(1)求证:AC2=AEAB;
(2)过点B作⊙O的切线交EC的延长线于点P,试判断PB与PE是否相等,并说明理由;
(3)设⊙O半径为4,点N为OC中点,点Q在⊙O上,求线段PQ的最小值.
相关试题

