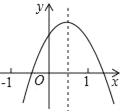
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0;⑤4ac﹣b2<0,正确的序号是_____.
参考答案:
【答案】②③⑤.
【解析】令x=1,y=a+b+c>0,
故①错误;
令x=1,y=ab+c<0,
故②正确;
由于对称轴x=![]() <1,a<0,
<1,a<0,
∴b>2a,
∴2a+b<0,
故③正确;
由图象可知:a<0,c>0,
对称轴:x=![]() >0,
>0,
∴b>0
∴abc<0,
故④错误;
由于抛物线与x轴有两个交点,
∴△=b4ac>0,
即4acb<0,故⑤正确;
故答案为:②③⑤
点睛: 此题考查了二次函数图象与系数的关系,以及二次函数的性质,熟练掌握二次函数的性质是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
-
科目: 来源: 题型:
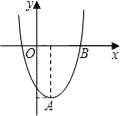
查看答案和解析>>【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1)、P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且﹣1<x1<x2,x3<﹣1,则y1、y2、y3的大小关系为( )

A. y1<y2<y3 B. y3<y1<y2 C. y3<y2<y1 D. y2<y1<y3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图①,在△ABC中,∠ACB=2∠B,AD为∠BAC的角平分线,
求证:AB=AC+CD
小明同学经过思考,得到如下解题思路:
在AB上截取AE=AC,连接DE,得到△ADE≌△ADC,从而易证AB=AC+CD
(1)请你根据以上解思路写出证明过程;
(2)如图②,若AD为△ABC的外角∠CAE平分线,交BC的延长线于点D,
∠D=25°,其他条件不变,求∠B的度数。


-
科目: 来源: 题型:
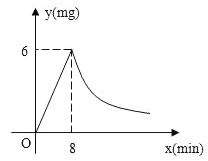
查看答案和解析>>【题目】为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
-
科目: 来源: 题型:
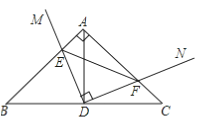
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
A. ①②④ B. ②③④
C. ①②③ D. ①②③④
相关试题

