【题目】如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
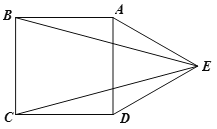
(1)求证:BE=CE.
(2)求∠BEC的度数
参考答案:
【答案】(1)证明见解析;(2)30°
【解析】
试题分析:(1)由正方形和等边三角形的性质得出AB=AE,DC=DE,∠BAE=150°,∠CDE=150°,可证ΔBAE≌ΔCDE,即可证出BE=CE;
(2)由(1)知:∠AEB=∠CED=15°,从而可求∠BEC的度数.
试题解析:(1)证明:∵四边形ABCD为正方形
∴AB=AD=CD,∠BAD=∠ ADC=90°
∵三角形ADE为正三角形
∴ AE=AD=DE,∠EAD=∠EDA=60°
∴∠BAE=∠CDE=150°
∴ΔBAE≌ΔCDE
∴BE=CE
(2)∵AB=AD, AD=AE,
∴AB=AE
∴∠ABE=∠AEB
又 ∵∠BAE=150° ∴∠ABE=∠AEB=15°
同理:∠CED=15°
∴∠BEC=600-15°×2=30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现:如图①,直线AB∥CD,E是AB与CD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
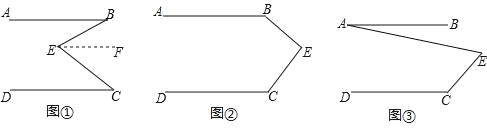
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C= (等式性质)
即∠B+∠C=∠BEC.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°﹣∠BEC.
(3)解决问题:如图③,AB∥DC,试写出∠A、∠C、∠AEC的数量关系 .(直接写出结论,不用写计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中是圆弧形拱桥,某天测得水面
 宽
宽 ,此时圆弧最高点距水面
,此时圆弧最高点距水面 .
.(
 )确定圆弧所在圆的圆心
)确定圆弧所在圆的圆心 .(尺规作图,保留作图痕迹)
.(尺规作图,保留作图痕迹)(
 )求圆弧所在圆的半径.
)求圆弧所在圆的半径.(
 )水面上升
)水面上升 ,水面宽__________
,水面宽__________  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
 半径为
半径为 ,
, 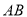 是⊙
是⊙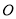 的直径,
的直径, 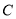 是⊙
是⊙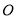 上一点,连接
上一点,连接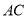 ,⊙
,⊙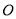 外的一点
外的一点 在直线
在直线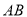 上.
上.(
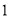 )若
)若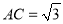 ,
, 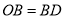 .
.①求证:
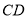 是⊙
是⊙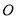 的切线.
的切线.②阴影部分的面积是__________.(结果保留
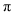 )
)(
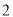 )当点
)当点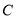 在⊙
在⊙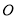 上运动时,若
上运动时,若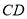 是⊙
是⊙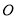 的切线,探究
的切线,探究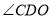 与
与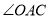 的数量关系.
的数量关系.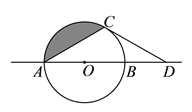
相关试题

