【题目】图中是圆弧形拱桥,某天测得水面![]() 宽
宽![]() ,此时圆弧最高点距水面
,此时圆弧最高点距水面![]() .
.
(![]() )确定圆弧所在圆的圆心
)确定圆弧所在圆的圆心![]() .(尺规作图,保留作图痕迹)
.(尺规作图,保留作图痕迹)
(![]() )求圆弧所在圆的半径.
)求圆弧所在圆的半径.
(![]() )水面上升
)水面上升![]() ,水面宽__________
,水面宽__________ ![]() .
.

参考答案:
【答案】![]()
【解析】试题分析:(![]() )作AB的垂直平分线CD交弧AB于C,连接AC,再作AC的垂直平分线交直线CD于点O,则点O就是所求的点.
)作AB的垂直平分线CD交弧AB于C,连接AC,再作AC的垂直平分线交直线CD于点O,则点O就是所求的点.
(2)设圆弧拱桥最高点为![]() ,连接
,连接![]() 、
、![]() 交
交![]() 于
于![]() ,由垂径定理得到:AD=10,在Rt△ADO中,用勾股定理即可得到结论;
,由垂径定理得到:AD=10,在Rt△ADO中,用勾股定理即可得到结论;
(3)水面上升至![]() 处,则
处,则![]() 为
为![]() 中点,
中点, ![]() ,得到OG=10,再用勾股定理和垂径定理即可得到结论.
,得到OG=10,再用勾股定理和垂径定理即可得到结论.
试题解析:解:(1)如图.

(2)设圆弧拱桥最高点为![]() ,连接
,连接![]() 、
、![]() 交
交![]() 于
于![]() ,
,

则![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 中:
中: ![]() ,
,
即![]() ,
, ![]() ,
,
∴![]() ,
,
即圆半径为![]() .
.
(3)水面上升至![]() 处,则
处,则![]() 为
为![]() 中点,
中点, ![]() ,
,

![]() ,
,
∴![]() ,
,
![]() 中:
中: ![]() ,
,
∴![]() ,
,
即水面宽![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE="10," 求直角梯形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
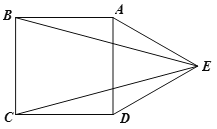
(1)求证:BE=CE.
(2)求∠BEC的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
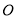 半径为
半径为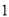 ,
,  是⊙
是⊙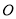 的直径,
的直径, 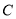 是⊙
是⊙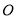 上一点,连接
上一点,连接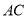 ,⊙
,⊙ 外的一点
外的一点 在直线
在直线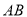 上.
上.(
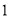 )若
)若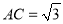 ,
, 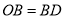 .
.①求证:
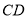 是⊙
是⊙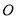 的切线.
的切线.②阴影部分的面积是__________.(结果保留
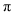 )
)(
 )当点
)当点 在⊙
在⊙ 上运动时,若
上运动时,若 是⊙
是⊙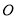 的切线,探究
的切线,探究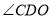 与
与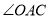 的数量关系.
的数量关系.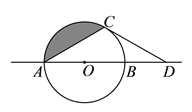
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙
 半径为
半径为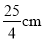 ,
,  是⊙
是⊙ 的直径,点
的直径,点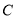 为
为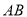 延长线上一点,动点
延长线上一点,动点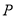 从点
从点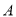 出发以
出发以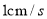 的速度沿
的速度沿 方向运动,同时,动点
方向运动,同时,动点 从点
从点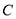 出发以
出发以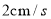 的速度沿
的速度沿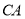 方向运动,当两点相遇时都停止运动.过点
方向运动,当两点相遇时都停止运动.过点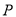 作
作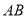 的垂线,与⊙
的垂线,与⊙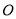 分别交于点
分别交于点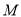 、
、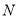 ,设点
,设点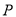 的运动时间为
的运动时间为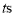 .
.(
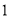 )当四边形
)当四边形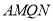 是正方形时,
是正方形时, 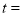 __________
__________ 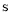 ,
, 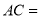 __________
__________  .
.(
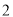 )当四边形
)当四边形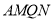 是菱形且
是菱形且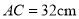 时,求
时,求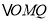 内切圆的半径.
内切圆的半径.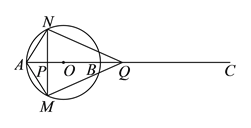
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是 (填序号).

相关试题

