搜索
【题目】我们知道分数
写为小数即
，反之，无限循环小数写成分数即．
一般地，任何一个无限循环小数都可以写成分数形式．
例如：把
写成分数形式时，设
=，则=0.5555…＝0.5＋0.05555…＝
解一元一次方程
，解得：
，所以=
．
（1）模仿上述过程，把无限循环小数0.
写成分数形式；
（2）你能把无限循环小数
化成分数形式吗？
参考答案：
【答案】（1）
；（2）
【解析】
根据例题可设x=0.
，则x=0.7777…①，再根据等式性质得：10x=7.777…②，然后利用②-①，再解方程即可．
（2）设x=0.5˙6˙，则x=0.5656…①，根据等式性质得：100x=56.5656…②，再由②-①得方程，再解方程即可．
(1)设x=0.，则x=0.7777…①，
根据等式性质得：10x=7.777…②，
由②①得：10xx=7.777…0.777…，
即：10xx=7，
解方程得：x=；
(2)设x=0.
，x=0.5656…①，
根据等式性质得：100x=56.5656…②，
由②①得：100xx=56.5656…0.5656…，
即：100xx=56，
解方程得：x=.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果事件A发生的概率是
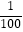，那么在相同条件下重复试验，下列4种陈述中，不正确的有 ①说明做100次这种试验，事件A必发生1次
②说明事件A发生的频率是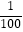
③说明做100次这种试验中，前99次事件A没发生，后1次事件A才发生
④说明做100次这种试验，事件A可能发生1次（ ）
A.①、②、③
B.①、②、④
C.②、③、④
D.①、②、③、④ -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料：
点A、B在数轴上分别表示两个数a、b，A、B两点间的距离记为|AB|，O表示原点．当A、B两点中有一点在原点时，不妨设点A为原点，如图1，则|AB|=|OB|=|b|=|a-b|；当A、B两点都不在原点时，
①如图2，若点A、B都在原点的右边时，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
②如图3，若点A、B都在原点的左边时，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；
③如图4，若点A、B在原点的两边时，|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|．
回答下列问题：
（1）综上所述，数轴上A、B两点间的距离为|AB|=______．
（2）若数轴上的点A表示的数为3，点B表示的数为-4，则A、B两点间的距离为______；
（3）若数轴上的点A表示的数为x，点B表示的数为-2，则|AB|=______，若|AB|=3，则x的值为______．
-
科目： 来源： 题型：
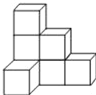
查看答案和解析>>【题目】在桌面上，有7个完全相同的小正方体堆成的一个几何体A，如图所示.
(1) 请画出这个几何体A的三视图.
(2) 若将此几何体的表面喷上红漆(放在桌面上的一面不喷)，则三个面上是红色的小正方体有______个.
(3) 若现在你的手头还有一些相同的小正方体可添放在该几何体上，要保持俯视图和左视图不变，则最多可以添加_______个小正方体.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AC=BC，∠C=90°，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，求证：DE=DF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，请你观察下列几种简单多面体模型，解答下列问题：
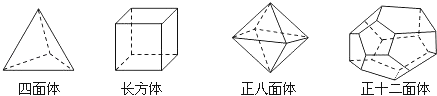
图1 图2
（探索新知）如图1，（1）根据上面多面体模型，完成表格中的空格；
多面体
顶点数（V）
面数（F）
棱数（E）
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是 ．
（2）根据以上关系式猜想是否存在一个多面体，它有16个面，50条棱，34个顶点？并写出理由。
（实际应用）如图2，足球一般有32块黑白皮子缝合而成，黑色的是正五边形，白色的是正六边形，如
果我们近似把足球看成一个多面体．
（1）设黑色的正五边形有x块，则白色的正六边形有（32﹣x）块，当把足球看成一个多面体时，它的棱数是 ，它的顶点数是 ．
（2）求出黑皮和白皮各有多少块？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，BC=9，AB的垂直平分线交BC与点M，AC的垂直平分线交BC于点N，则△AMN的周长=_____．
相关试题
