Question

【题目】如图，直线y=5x+5交x轴于点A，交y轴于点C，过A，C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B．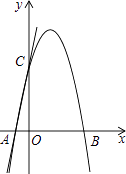

（1）求二次函数的表达式；
（2）连接BC，点N是线段BC上的动点，作ND⊥x轴交二次函数的图象于点D，求线段ND长度的最大值；
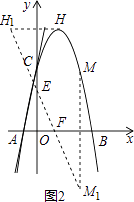
（3）若点H为二次函数y=ax2+4x+c图象的顶点，点M（4，m）是该二次函数图象上一点，在x轴、y轴上分别找点F，E，使四边形HEFM的周长最小，求出点F，E的坐标．
温馨提示：在直角坐标系中，若点P，Q的坐标分别为P（x1 ， y1），Q（x2 ， y2），
当PQ平行x轴时，线段PQ的长度可由公式PQ=|x1﹣x2|求出；
当PQ平行y轴时，线段PQ的长度可由公式PQ=|y1﹣y2|求出．

Answer 1

【答案】
（1）

解：∵直线y=5x+5交x轴于点A，交y轴于点C，

∴A（﹣1，0），C（0，5），

∵二次函数y=ax2+4x+c的图象过A，C两点，

∴ ，

解得 ，

∴二次函数的表达式为y=﹣x2+4x+5

（2）

解：如图1，

∵点B是二次函数的图象与x轴的交点，

∴由二次函数的表达式为y=﹣x2+4x+5得，点B的坐标B（5，0），

设直线BC解析式为y=kx+b，

∵直线BC过点B（5，0），C（0，5），

∴ ，

解得 ，

∴直线BC解析式为y=﹣x+5，

设ND的长为d，N点的横坐标为n，

则N点的纵坐标为﹣n+5，D点的坐标为D（n，﹣n2+4n+5），

则d=|﹣n2+4n+5﹣（﹣n+5）|，

由题意可知：﹣n2+4n+5＞﹣n+5，

∴d=﹣n2+4n+5﹣（﹣n+5）=﹣n2+5n=﹣（n﹣ ）2+ ，

∴当n= 时，线段ND长度的最大值是

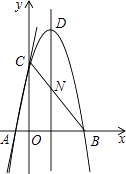
（3）

解：由题意可得二次函数的顶点坐标为H（2，9），点M的坐标为M（4，5），

作点H（2，9）关于y轴的对称点H1，则点H1的坐标为H1（﹣2，9），

作点M（4，5）关于x轴的对称点HM1，则点M1的坐标为M1（4，﹣5），

连结H1M1分别交x轴于点F，y轴于点E，

所以H1M1+HM的长度是四边形HEFM的最小周长，则点F、E即为所求，

设直线H1M1解析式为y=k1x+b1，

直线H1M1过点M1（4，﹣5），H1（﹣2，9），

根据题意得方程组 ，

解得 ，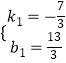

∴y=﹣ x+ ，

∴点F，E的坐标分别为（ ，0）（0， ）．

【解析】（1）先根据坐标轴上点的坐标特征由一次函数的表达式求出A，C两点的坐标，再根据待定系数法可求二次函数的表达式；（2）根据坐标轴上点的坐标特征由二次函数的表达式求出B点的坐标，根据待定系数法可求一次函数BC的表达式，设ND的长为d，N点的横坐标为n，则N点的纵坐标为﹣n+5，D点的坐标为D（n，﹣n2+4n+5），根据两点间的距离公式和二次函数的最值计算可求线段ND长度的最大值；（3）由题意可得二次函数的顶点坐标为H（2，9），点M的坐标为M（4，5），作点H（2，9）关于y轴的对称点H1 ， 可得点H1的坐标，作点M（4，5）关于x轴的对称点HM1 ， 可得点M1的坐标连结H1M1分别交x轴于点F，y轴于点E，可得H1M1+HM的长度是四边形HEFM的最小周长，再根据待定系数法可求直线H1M1解析式，根据坐标轴上点的坐标特征可求点F、E的坐标．考查了二次函数综合题，涉及的知识点有：坐标轴上点的坐标特征，待定系数法求一次函数的表达式，待定系数法求二次函数的表达式，二次函数的顶点坐标，两点间的距离公式，二次函数的最值，轴对称﹣最短路线问题，方程思想的应用，综合性较强，有一定的难度．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．