【题目】把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( ) 
A.内部
B.外部
C.边上
D.以上都有可能
参考答案:
【答案】C
【解析】解:∵AC=BD=10,
又∵∠ABC=∠DEB=90°,∠A=45°,∠D=30°,
∴BE=5,AB=BC=5 ![]() ,
,
由三角板DEB绕点B逆时针旋转45°得到△D′E′B,设△D′E′B与直线AB交于G,可知:∠EBE′=45°,∠E′=∠DEB=90°,
∴△GE′B是等腰直角三角形,且BE′=BE=5,
∴BG= ![]() =5
=5 ![]() ,
,
∴BG=AB,
∴点A在△D′E′B的边上,
故选C.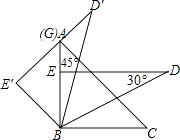
先根据勾股定理求出两直角三角形的各边长,再由旋转的性质得:∠EBE′=45°,∠E′=∠DEB=90°,求出E′D′与直线AB的交点到B的距离也是5 ![]() ,与AB的值相等,所以点A在△D′E′B的边上.本题考查了旋转的性质和勾股定理,利用30°和45°的直角三角形的性质求出各边的长;注意:在直角三角形中,30度角所对的直角边等于斜边的一半,45°角所对的两直角边相等,熟练掌握此内容是解决问题的关键.
,与AB的值相等,所以点A在△D′E′B的边上.本题考查了旋转的性质和勾股定理,利用30°和45°的直角三角形的性质求出各边的长;注意:在直角三角形中,30度角所对的直角边等于斜边的一半,45°角所对的两直角边相等,熟练掌握此内容是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.
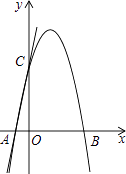
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴、y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.
温馨提示:在直角坐标系中,若点P,Q的坐标分别为P(x1 , y1),Q(x2 , y2),
当PQ平行x轴时,线段PQ的长度可由公式PQ=|x1﹣x2|求出;
当PQ平行y轴时,线段PQ的长度可由公式PQ=|y1﹣y2|求出. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是⊙O的直径,已知∠1=30°,则∠2=( )

A.30°
B.45°
C.60°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,D为△ABC的边AB的延长线上一点,过D作DF⊥AC,垂足为F,交BC于E,且BD=BE,求证:△ABC是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(阴影部分)面积之和为S2 , 则
 =( )
=( ) 
A.
B.
C.
D.1
相关试题

