【题目】关于x的方程mx2﹣2x+1=0有实数解,则m需满足 .
参考答案:
【答案】m≤1
【解析】解:∵方程mx2﹣2x+1=0有实数解,∴△=(﹣2)2﹣4m=4﹣4m≥0,
解得:m≤1.
所以答案是:m≤1.
【考点精析】根据题目的已知条件,利用求根公式的相关知识可以得到问题的答案,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x,-4)与点B(3,y)关于y轴对称,那么x+y的值为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣4x+5的顶点坐标为( )
A.(﹣2,﹣1)
B.(2,1)
C.(2,﹣1)
D.(﹣2,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】2008年爆发的世界金融危机,是自上世纪三十年代以来世界最严重的一场金融危机.受金融危机的影响,某商品原价为200元,连续两次降价a%后售价为148元,下面所列方程正确的是( )
A.200(1+a%)2=148
B.200(1﹣a%)2=148
C.200(1﹣2a%)=148
D.200(1﹣a2%)=148 -
科目: 来源: 题型:
查看答案和解析>>【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了
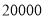
 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为
天的总成本为 万元;放养
万元;放养 天的总成本为
天的总成本为 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).(1)设每天的放养费用是
 万元,收购成本为
万元,收购成本为 万元,求
万元,求 和
和 的值;
的值;(2)设这批淡水鱼放养
 天后的质量为
天后的质量为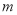 (
(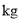 ),销售单价为
),销售单价为 元/
元/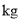 .根据以往经验可知:
.根据以往经验可知: 与
与 的函数关系为
的函数关系为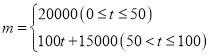 ;
; 与
与 的函数关系如图所示.
的函数关系如图所示.①分别求出当
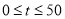 和
和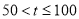 时,
时, 与
与 的函数关系式;
的函数关系式;②设将这批淡水鱼放养
 天后一次性出售所得利润为
天后一次性出售所得利润为 元,求当
元,求当 为何值时,
为何值时, 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 .
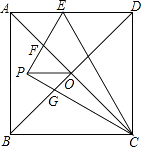
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘潜水艇所在的海拔高度为﹣50m,若一条鲨鱼在潜水艇下方10m处,则鲨鱼所在的海拔高度为_____.
相关试题

