【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
① △ABE的面积与△BCE的面积相等;② ∠AFG=∠AGF;③ ∠FAG=2∠ACF;④ BH=CH

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
参考答案:
【答案】A
【解析】根据三角形中线的性质可得:△ABE的面积和△BCE的面积相等,故①正确,
因为∠BAC=90°,所以∠AFG+∠ACF=90°,因为AD是高,所以∠DGC+∠DCG=90°,
因为CF是角平分线,所以∠ACF=∠DCG,所以∠AFG=∠DGC,又因为∠DGC=∠AGF,所以
∠AFG=∠AGF,故②正确,
因为∠FAG+∠ABC=90°, ∠ACB+∠ABC=90°,所以∠FAG=∠ACB,又因为CF是角平分线,所以∠ACB=2∠ACF,所以∠FAG=2∠ACF,故③正确,
④假设BH=CH, ∠ACB=30°,则∠HBC=∠HCB =15°, ∠ABC=60°,
所以∠ABE=60°-15°=45°,因为∠BAC=90°,所以AB=AE,因为AE=EC,所以AB=![]() ,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
,这与在直角三角形中30°所对直角边等于斜边的一半相矛盾,所以假设不成立,故④不一定正确,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进营业额不断增长,某大型超市决定购进甲、乙两种商品,已知甲种商品每件进价为150元,售价为168元;乙种商品每件进价为120元,售价为140元,该超市用42000元购进甲、乙两种商品,销售完后共获利5600元.
(1)该超市购进甲、乙两种商品各多少件?
(2)超市第二次以原价购进甲、乙两种商品共400件,且购进甲种商品的件数多于乙种商品的件数,要使第二次经营活动的获利不少于7580元,共有几种进货方案?写出利润最大的进货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-x-1的图象不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是﹣2.
已知点A是数轴上的点,完成下列各题: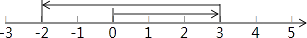
(1)如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是 , A、B两点间的距离为;
(2)如果点A表示的数是﹣4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是 , A、B两点间的距离为;
一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是 , A、B两点间的距离为 . -
科目: 来源: 题型:
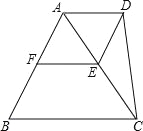
查看答案和解析>>【题目】如图,点E、F分别是等边△ABC中AC、AB边上的中点,以AE为边向外作等边△ADE.
(1)求证:四边形AFED是菱形;
(2)连接DC,若BC=10,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解决有关问题:我们知道|x|=
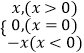 ,
,
所以当x>0时,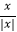 =
= 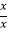 =1; 当x<0时,
=1; 当x<0时, 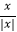 =
=  =﹣1.现在我们可以用这个结论来解决下面问题:
=﹣1.现在我们可以用这个结论来解决下面问题:
(1)已知a,b是有理数,当ab≠0时,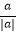 +
+ 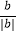 =;
=;
(2)已知a,b是有理数,当abc≠0时,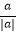 +
+ 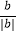 +
+ 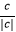 =;
=;
(3)已知a,b,c是有理数,a+b+c=0,abc<0,则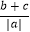 +
+ 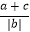 +
+ 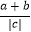 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
①﹣|﹣ |=
|=
②﹣(﹣6)=
③(﹣1)99= .
相关试题

