搜索
【题目】如图，一次函数y1=kx+b的图象与反比例函数y2= 
的图象相交于点A（2，3）和点B，与x轴相交于点C（8，0）．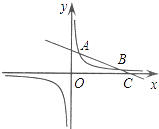 
（1）求这两个函数的解析式；
（2）当x取何值时，y1＞y2 ．
参考答案：
【答案】
（1）解：把 A（2，3）代入y2= 
，得m=6．
∴y2= 
，
把 A（2，3）、C（8，0）代入y1=kx+b，
得 
，
∴这两个函数的解析式为y1=﹣ 
x+4，y2=
（2）解：由题意得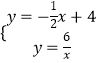 
，
解得 
， 
，
当x＜0 或 2＜x＜6 时，y1＞y2
【解析】（1）将A、B中的一点代入y2= ，即可求出m的值，从而得到反比例函数解析式，把 A（2，3）、C（8，0）代入y1=kx+b，可得到k、b的值；（2）根据图象可直接得到y1＞y2时x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算与解方程
（1）计算：（π﹣3）0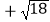
﹣2sin45°﹣（ 
）﹣1 ．
（2）解方程：x（x﹣6）=﹣9． -
科目： 来源： 题型：
查看答案和解析>>【题目】请根据图示的对话解答下列问题．
求：（1）a，b的值；
（2）8﹣a+b﹣c的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是用长度相等的小棒按一定规律摆成的一组图案．
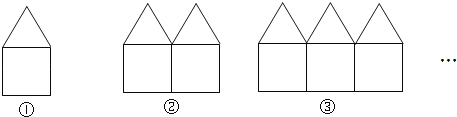
（1）第1个图案中有______根小棒；第2个图案中有__根小棒；第3个图案中有__根小棒；
（2）第n个图案中有多少根小棒？
（3）第25个图案中有多少根小棒？
（4）是否存在某个符合上述规律的图案，由2032根小棒摆成？如果有，指出是第几个图案；如果没有，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】目前，步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗．对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同．若每消耗1千卡能量小明行走的步数比小红多10步，求小红每消耗1千卡能量需要行走多少步？
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了弘扬“社会主义核心价值观”，市政府在广场树立公益广告牌，如图所示，为固定广告牌，在两侧加固钢缆，已知钢缆底端D距广告牌立柱距离CD为3米，从D点测得广告牌顶端A点和底端B点的仰角分别是60°和45°．
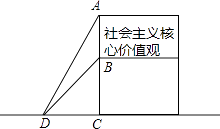
（1）求公益广告牌的高度AB；
（2）求加固钢缆AD和BD的长．（注意：本题中的计算过程和结果均保留根号） -
科目： 来源： 题型：
查看答案和解析>>【题目】目前，步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗．对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同．若每消耗1千卡能量小明行走的步数比小红多10步，求小红每消耗1千卡能量需要行走多少步？
【答案】小红每消耗1千卡能量需要行走30步．
【解析】分析：设小红每消耗1千卡能量需要行走x步，则小明每消耗1千卡能量需要行走（x+10）步，根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数结合小明步行12000步与小红步行9000步消耗的能量相同，即可得出关于x的分式方程，解之后经检验即可得出结论．
详解：设小红每消耗1千卡能量需要行走x步，则小明每消耗1千卡能量需要行走（x+10）步，
根据题意，得
，
解得x=30．
经检验：x=30是原方程的解．
答：小红每消耗1千卡能量需要行走30步．点睛：本题考查了分式方程的应用，根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数列出关于x的分式方程是解题的关键．
【题型】解答题
【结束】
25【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于F，连接CF．
（1）求证：四边形ADCF是平行四边形；
（2）当△ABC满足什么条件时，四边形ADCF为正方形，请你添加适当的条件并证明你的结论．
相关试题
