【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
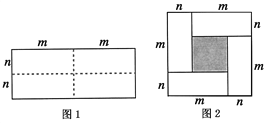
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求:
,求:![]() 的值;
的值;
②已知:![]() ,
,![]() ,求:
,求:![]() 的值.
的值.
参考答案:
【答案】(1)方法1:(m﹣n)2;方法2:(m+n)2﹣4mn;
(2)(m﹣n)2;(m+n)2﹣4mn;(m﹣n)2=(m+n)2﹣4mn;
(3)①1;②3.
【解析】试题分析:(1)表示出阴影部分的边长,然后利用正方形的面积公式列式;
利用大正方形的面积减去四周四个矩形的面积列式;
(2)根据不同方法表示的阴影部分的面积相同解答;
(3)根据(2)的结论代入进行计算即可得解.
解:(1)方法1:(m﹣n)2;
方法2:(m+n)2﹣4mn;
(2)(m﹣n)2=(m+n)2﹣4mn;
故答案为:(m﹣n)2;(m+n)2﹣4mn;(m﹣n)2=(m+n)2﹣4mn;
(3)①解:∵a﹣b=5,ab=﹣6,
∴(a+b)2=(a﹣b)2+4ab=52+4×(﹣6)=25﹣24=1;
②解:由已知得:(a+)2=(a﹣)2+4a=12+8=9,
∵a>0,a+>0,
∴a+=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】海图中,如果用1cm表示20 n mile,那么32 n mile在图上显示为________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程ax﹣6=2的解为=﹣2,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知AB∥CD,EF⊥AB于点O,∠FGC=125°,求∠EFG的度数.

下面提供三种思路:
(1)过点F作FH∥AB;
(2)延长EF交CD于M;
(3)延长GF交AB于K.
请你利用三个思路中的两个思路,
将图形补充完整,求∠EFG的度数.
解(一):
解(二):
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴交与A(4,0),并且OA=OC=4OB,点P为过A、B、C三点的抛物线上一动点.
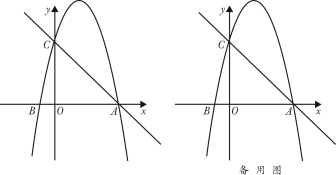
(1)、求点B、点C的坐标并求此抛物线的解析式;
(2)、是否存在点P,使得△ACP是以点C为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)、过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣2y2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】23表示( )
A.2×2×2
B.2×3
C.3×3
D.2+2+2
相关试题

