【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
试题分析:根据勾股定理的逆定理可以证明∠BAC=90°;根据直角三角形斜边上的中线等于斜边的一半,则AM=![]() EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
解:∵在△ABC中,AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
即∠BAC=90°.
又∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=![]() EF=
EF=![]() AP.
AP.
因为AP的最小值即为直角三角形ABC斜边上的高,即等于![]() ,
,
∴AM的最小值是![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是直角三角形,∠ACB=90°

(1)利用尺规作∠ABC 的平分线,交AC 于点O,再以O 为圆心,OC 的长为半径作⊙O(保留作图痕迹,不写作法);
(2)在你所作的图中,①判断AB 与⊙O 的位置关系,并证明你的结论;②若AC=12,tan∠OBC=
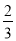 ,求⊙O 的半径。
,求⊙O 的半径。 -
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.

(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】认真阅读材料,然后回答问题:我们初中学习了多项式的运算法则,相应的我们可以计算出多项式的展开式,如:(a+b)1=a+b,
(a+b)2=a2+2ab+b2,(a+b)3=a3+3a2b+3ab2+b3,…下面我们依次对(a+b)n展开式的各项系数进一步研究发现,当n取正整数是可以单独列成表中的形式:

上面的多项式展开系数表称为“杨辉三角形”;仔细观察“杨辉三角形”,用你发现的规律回答下列问题:(1)
 展开式中共有多少项?
展开式中共有多少项?(2)请写出多项式
 的展开式?
的展开式? -
科目: 来源: 题型:
查看答案和解析>>【题目】命题:①邻补角互补;②对顶角相等;③同旁内角互补;④两点之间线段最短.其中真命题的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

