Question

【题目】如图，△ABC是等边三角形，AB=4cm，CD⊥AB于点D，动点P从点A出发，沿AC以2cm/s的速度向终点C运动，当点P出发后，过点P作PQ∥BC交折线AD﹣DC于点Q，以PQ为边作等边三角形PQR，设四边形APRQ与△ACD重叠部分图形的面积为S（cm2），点P运动的时间为t（s）．

（1）当点Q在线段AD上时，用含t的代数式表示QR的长；
（2）求点R运动的路程长；
（3）当点Q在线段AD上时，求S与t之间的函数关系式；
（4）直接写出以点B，Q，R为顶点的三角形是直角三角形时t的值．

Answer 1

【答案】
（1）

解：如图①，

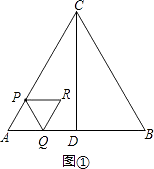
∵△ABC是等边三角形，

∴∠ACB=∠B=60°．

∵PQ∥BC，

∴∠APQ=∠ACB=60°，∠AQP=∠B=60°，

∴△APQ是等边三角形．

∴PQ=AP=2t．

∵△PQR是等边三角形，

∴QR=PQ=2t

（2）

解：过点A作AG⊥BC于点G，如图②，

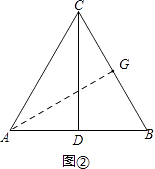
则点R运动的路程长是AG+CG．

在Rt△AGC中，∠AGC=90°，sin60°= = ，cos60°= = ，AC=4，

∴AG=2 ，CG=2．

∴点R运动的路程长2 +2

（3）

解：①当0＜t≤ 时，如图③，

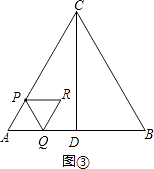
S=S菱形APRQ=2×S正△APQ=2× ×（2t）2=2 t2；

②当 ＜t≤1时，如图④

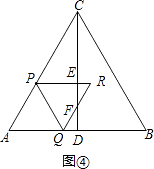
PE=PCsin∠PCE=（4﹣2t）× =2﹣t，

∴ER=PR﹣PE=2t﹣（2﹣t）=3t﹣2，

∴EF=ERtanR= （3t﹣2）

∴S=S菱形APRQ﹣S△REF

=2 t2﹣ （3t﹣2）2=﹣ t2+6 t﹣2

（4）

解：t= 或t=

提示：①当∠QRB=90°时，如图⑤，

cos∠RQB= = ，

∴QB=2QR=2QA，

∴AB=3QA=6t=4，

∴t= ；

②当∠RQB=90°时，如图⑥，

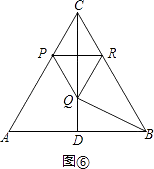
同理可得BC=3RC=3PC=3（4﹣2t）=4，

∴t=

【解析】（1）易证△APQ是等边三角形，即可得到QR=PQ=AP=2t；（2）过点A作AG⊥BC于点G，如图②，易得点R运动的路程长是AG+CG，只需求出AG、CG就可解决问题；（3）四边形APRQ与△ACD重叠部分图形可能是菱形，也可能是五边形，故需分情况讨论，然后运用割补法就可解决问题；（4）由于直角顶点不确定，故需分情况讨论，只需分∠QRB=90°和∠RQB=90°两种情况讨论，即可解决问题．