【题目】已知:如图,抛物线y=a(x﹣1)2+c与x轴交于点A( ![]() ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处.
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点P′(1,3)处. 
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P′作x轴的平行线交抛物线于C,D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比 ![]() (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据: ![]() ,
, ![]() ,结果可保留根号)
,结果可保留根号)
参考答案:
【答案】
(1)解:∵P与P′(1,3)关于x轴对称,
∴P点坐标为(1,﹣3);
∵抛物线y=a(x﹣1)2+c过点A( ![]() ,0),顶点是P(1,﹣3),
,0),顶点是P(1,﹣3),
∴ ![]() ;
;
解得 ![]() ;
;
则抛物线的解析式为y=(x﹣1)2﹣3,
即y=x2﹣2x﹣2
(2)解:∵CD平行x轴,P′(1,3)在CD上,
∴C、D两点纵坐标为3;
由(x﹣1)2﹣3=3,
解得: ![]() ,
, ![]() ,
,
∴C、D两点的坐标分别为( ![]() ,3),(
,3),( ![]() ,3)
,3)
∴CD= ![]()
∴“W”图案的高与宽(CD)的比= ![]() (或约等于0.6124)
(或约等于0.6124)
【解析】(1)利用P与P′(1,3)关于x轴对称,得出P点坐标,利用待定系数法求出二次函数的解析式即可;(2)根据已知得出C,D两点坐标,进而得出“W”图案的高与宽(CD)的比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y1=x,y2=
 x+1,y3=﹣
x+1,y3=﹣ 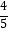 x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为
x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为 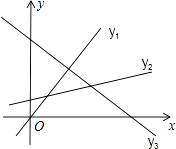
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.23=6
B.﹣42=﹣16
C.﹣8﹣8=0
D.﹣5﹣2=﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对量中,不具有相反意义的是( )
A. 盈利3万元与支出3万元
B. 胜2局与负2局
C. 向东走100m与向西走50m
D. 转盘逆时针转6圈与顺时针转6圈
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一粒大米的质量约为0.0000021千克,这个数用科学记数法表示为( )
A.0.21×10﹣5
B.2.1×10﹣5
C.2.1×10﹣6
D.21×10﹣6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a|=a,下列各式成立的是( )
A.a>0
B.a<0
C.a≥0
D.a≤0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以2cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD﹣DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).

(1)当点Q在线段AD上时,用含t的代数式表示QR的长;
(2)求点R运动的路程长;
(3)当点Q在线段AD上时,求S与t之间的函数关系式;
(4)直接写出以点B,Q,R为顶点的三角形是直角三角形时t的值.
相关试题

