【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
参考答案:
【答案】(1)6;(2)![]() 的值为
的值为![]() 或
或![]() ;(3)当
;(3)当![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
(1)根据勾股定理可以得到AC;
(2)过![]() 作
作![]() 于
于![]() ,求出AD=2,设
,求出AD=2,设![]() ,则
,则![]() ,根据勾股定理求出CP,根据P所走的路径为AB,BC,CP之和,求出t即可,注意P,D重合时也符合题意P所走的路径为AB,求出t即可.
,根据勾股定理求出CP,根据P所走的路径为AB,BC,CP之和,求出t即可,注意P,D重合时也符合题意P所走的路径为AB,求出t即可.
(3)①当![]() 在
在![]() 上且
上且![]() 时,根据
时,根据![]() ,而
,而![]() ,
,![]() ,求出CP=BP ,P为AB中点,即可求出;
,求出CP=BP ,P为AB中点,即可求出;
②当![]() 在
在![]() 上且
上且![]() 时,直接求出即可;
时,直接求出即可;
③当![]() 在
在![]() 上且
上且![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,根据△ADC∽△ACB,求出AD,即可求出AB,即可求出;
,根据△ADC∽△ACB,求出AD,即可求出AB,即可求出;
④当![]() 在
在![]() 上且
上且![]() 时,
时,![]() ,即可求出.
,即可求出.
解:(1)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
故答案为:![]() ;
;
(2)如图,过![]() 作
作![]() 于
于![]() ,
,
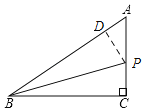
![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
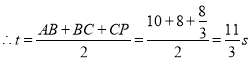 ;
;
当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 也在
也在![]() 的角平分线上,
的角平分线上,
此时,![]() ;
;
综上所述,点![]() 恰好在
恰好在![]() 的角平分线上,
的角平分线上,![]() 的值为
的值为![]() 或
或![]() ;
;
(3)分四种情况:
①如图,当![]() 在
在![]() 上且
上且![]() 时,
时,
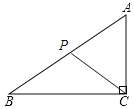
![]() ,而
,而![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,即
的中点,即![]() ,
,
![]() ;
;
②如图,当![]() 在
在![]() 上且
上且![]() 时,
时,
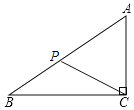
![]() ;
;
③如图,当![]() 在
在![]() 上且
上且![]() 时,过
时,过![]() 作
作![]() 于
于![]() ,则
,则
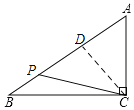
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() ;
;
④如图,当![]() 在
在![]() 上且
上且![]() 时,
时,![]() ,
,
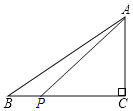
![]() .
.
综上所述,当![]() 或
或![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数
频率
体育
40
0.4
科技
25
a
艺术
b
0.15
其它
20
0.2
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
已知:如图,在正方形ABCD中,边AB=a1.
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
操作步骤
作法
由操作步骤推断(仅选取部分结论)
第一步
在第一个正方形ABCD的对角线AC上截取AE=a1,再作EF⊥AC于点E,EF与边BC交于点F,记CE=a2
(i)△EAF≌△BAF(判定依据是①);
(ii)△CEF是等腰直角三角形;
(iii)用含a1的式子表示a2为②:
第二步
以CE为边构造第二个正方形CEFG;
第三步
在第二个正方形的对角线CF上截取FH=a2,再作IH⊥CF于点H,IH与边CE交于点I,记CH=a3:
(iv)用只含a1的式子表示a3为③:
第四步
以CH为边构造第三个正方形CHIJ
这个过程可以不断进行下去.若第n个正方形的边长为an,用只含a1的式子表示an为④
请解决以下问题:
(1)完成表格中的填空:
① ;② ;③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
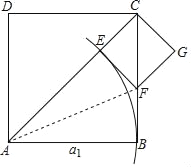
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=
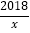 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为

A. 4 B.
 C. 6 D.
C. 6 D. 
相关试题

