【题目】已知AB=AC,BD=DC,AE平分∠FAB,问:AE与AD是否垂直?为什么? 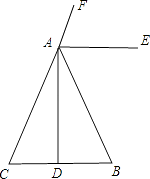
参考答案:
【答案】证明:∵AB=AC,CD=BD,
∴∠1=∠2,∠B=∠C,AD⊥BC,
又∵AE是△ABC的外角平分线,
∴∠3=∠4= ![]() (∠B+∠C)=∠C,
(∠B+∠C)=∠C,
∴AE∥BC,∠DAE+∠ADB=180°,
又∵AD⊥BC,
∴∠DAE=∠ADC=90°.
∴AE⊥AD.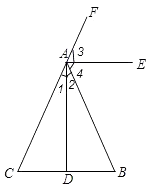
【解析】根据等腰三角形的性质可知,∠1=∠2,∠B=∠C,由三角形外角平分线的性质可知∠3=∠C,AE∥BC,由平行线的性质可知AE⊥AD.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】当代数式x2+3x+5的值等于7时,代数式3x2+9x﹣2的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数1,0,﹣1,﹣2中,最小的数是( )
A.1
B.0
C.﹣1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
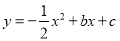 与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)作Rt△OBC的高OD,延长OD与抛物线在第一象限内交于点E,求点E的坐标;
(3)①在x轴上方的抛物线上,是否存在一点P,使四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由;
②在抛物线的对称轴上,是否存在上点Q,使得△BEQ的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
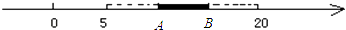
(1)若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为cm.
(2)由题(1)的启发,请你能借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣3﹣(﹣4)+2;
(2)(﹣6)÷2×(﹣ );
);
(3)(﹣ +
+  ﹣
﹣ 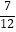 )×(﹣24);
)×(﹣24);
(4)﹣14﹣7÷[2﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+bx+c的图象上有两点(3,4)和(﹣5,4),则此抛物线的对称轴是直线x=
相关试题

